Merge pull request #2 from bmx-ng/task/add-new-generators

Added secure and prvhash random number generators.

prvhash.mod/examples/example_01.bmx

@@ -0,0 +1,10 @@
+SuperStrict
+
+Framework BRL.Standardio
+Import Random.prvhash
+
+SeedRnd(101)
+
+For Local i:Int = 0 until 30
+	Print RndDouble()
+Next

prvhash.mod/glue.c

@@ -0,0 +1,49 @@
+ /*
+  Copyright (c) 2023 Bruce A Henderson
+ 
+  Permission is hereby granted, free of charge, to any person obtaining a
+  copy of this software and associated documentation files (the "Software"),
+  to deal in the Software without restriction, including without limitation
+  the rights to use, copy, modify, merge, publish, distribute, sublicense,
+  and/or sell copies of the Software, and to permit persons to whom the
+  Software is furnished to do so, subject to the following conditions:
+ 
+  The above copyright notice and this permission notice shall be included in
+  all copies or substantial portions of the Software.
+ 
+  THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+  IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+  FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+  AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+  LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+  FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+  DEALINGS IN THE SOFTWARE.
+ */
+
+#include "prvhash_core.h"
+
+struct SState {
+    uint64_t seed;
+    uint64_t lcg;
+    uint64_t hash;
+};
+
+void bmx_prvhash_seed(uint64_t seed, struct SState * state) {
+    state->seed = seed;
+    state->lcg = 0;
+    state->hash = 0;
+
+    for (int i = 0; i < 5; i++)
+    {
+        prvhash_core64(&state->seed, &state->lcg, &state->hash);
+    }
+}
+
+uint64_t bmx_prvhash_next(struct SState * state) {
+    return prvhash_core64(&state->seed, &state->lcg, &state->hash);
+}
+
+double bmx_prvhash_next_double(struct SState * state) {
+    uint64_t rv = bmx_prvhash_next(state);
+    return ( rv >> ( 64 - 53 )) * 0x1p-53;
+}

prvhash.mod/prvhash.bmx

@@ -0,0 +1,128 @@
+' Copyright (c) 2023 Bruce A Henderson
+'
+' Permission is hereby granted, free of charge, to any person obtaining a
+' copy of this software and associated documentation files (the "Software"),
+' to deal in the Software without restriction, including without limitation
+' the rights to use, copy, modify, merge, publish, distribute, sublicense,
+' and/or sell copies of the Software, and to permit persons to whom the
+' Software is furnished to do so, subject to the following conditions:
+'
+' The above copyright notice and this permission notice shall be included in
+' all copies or substantial portions of the Software.
+'
+' THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+' IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+' FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+' AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+' LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+' FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+' DEALINGS IN THE SOFTWARE.
+'
+SuperStrict
+
+Rem
+bbdoc: Random Numbers - PRVHASH
+End Rem
+Module Random.PRVHASH
+
+ModuleInfo "Version: 1.00"
+ModuleInfo "License: MIT"
+ModuleInfo "Copyright: Wrapper - 2023 Bruce A Henderson"
+ModuleInfo "Copyright: PRVHASH - 2020-2023 Aleksey Vaneev"
+
+ModuleInfo "History: 1.00"
+ModuleInfo "History: Initial Release."
+
+Import Random.Core
+Import "prvhash/*.h"
+Import "glue.c"
+
+Type TPrvHashRandom Extends TRandom
+	
+	Private
+	
+	Field rnd_state:SHashState
+	Field rnd_seed:Int
+	
+	Public
+	
+	Method New()
+		SeedRnd(GenerateSeed())
+	End Method
+	
+	Method New(seed:Int)
+		SeedRnd seed
+	End Method
+	
+	Method RndFloat:Float()
+		Return Float(RndDouble())
+	End Method
+	
+	Method RndDouble:Double()
+		Return bmx_prvhash_next_double(rnd_state)
+	End Method
+	
+	Method Rnd:Double(minValue:Double = 1, maxValue:Double = 0)
+		If maxValue > minValue Return RndDouble() * (maxValue - minValue) + minValue
+		Return RndDouble() * (minValue - maxValue) + maxValue
+	End Method
+	
+	Method Rand:Int(minValue:Int, maxValue:Int = 1)
+		Local Range:Double = maxValue - minValue
+		If Range > 0 Return Int( bmx_prvhash_next_double(rnd_state)*(1:Double+Range) )+minValue
+		Return Int( bmx_prvhash_next_double(rnd_state)*(1:Double-Range) )+maxValue
+	End Method
+	
+	Method SeedRnd(seed:Int)
+		rnd_seed = seed
+		If seed = 0 Then
+			seed = $1234
+		End If
+		bmx_prvhash_seed(ULong(seed), rnd_state)
+	End Method
+	
+	Method RndSeed:Int()
+		Return rnd_seed
+	End Method
+
+	Method GetName:String()
+		Return "PRVHASH"
+	End Method
+
+End Type
+
+Private
+Type TPrvHashRandomFactory Extends TRandomFactory
+	
+	Method New()
+		Super.New()
+		Init()
+	End Method
+	
+	Method GetName:String()
+		Return "PRVHASH"
+	End Method
+	
+	Method Create:TRandom(seed:Int)
+		Return New TPrvHashRandom(seed)
+	End Method
+
+	Method Create:TRandom()
+		Return New TPrvHashRandom()
+	End Method
+		
+End Type
+
+Struct SHashState
+	Field seed:ULong
+	Field lcg:ULong
+	Field hash:ULong
+End Struct
+
+Extern
+	Function bmx_prvhash_seed(seed:ULong, state:SHashState Var)
+	Function bmx_prvhash_next:ULong(state:SHashState Var)
+	Function bmx_prvhash_next_double:Double(state:SHashState Var)
+End Extern
+
+New TPrvHashRandomFactory

prvhash.mod/prvhash/LICENSE

@@ -0,0 +1,21 @@
+MIT License
+
+Copyright (c) 2020-2023 Aleksey Vaneev
+
+Permission is hereby granted, free of charge, to any person obtaining a copy
+of this software and associated documentation files (the "Software"), to deal
+in the Software without restriction, including without limitation the rights
+to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
+copies of the Software, and to permit persons to whom the Software is
+furnished to do so, subject to the following conditions:
+
+The above copyright notice and this permission notice shall be included in all
+copies or substantial portions of the Software.
+
+THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
+OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
+SOFTWARE.

prvhash.mod/prvhash/README.md

@@ -0,0 +1,1079 @@
+# PRVHASH - Pseudo-Random-Value Hash #
+
+## Introduction ##
+
+PRVHASH is a hash function that generates a [uniform pseudo-random number
+sequence](https://en.wikipedia.org/wiki/Pseudorandom_number_generator)
+derived from the message. PRVHASH is conceptually similar (in the sense of
+using a pseudo-random number sequence as a hash) to [`keccak`](https://en.wikipedia.org/wiki/SHA-3)
+and [`RadioGatun`](https://en.wikipedia.org/wiki/RadioGat%C3%BAn)
+schemes, but is a completely different implementation of such concept.
+PRVHASH is both a ["randomness extractor"](https://en.wikipedia.org/wiki/Randomness_extractor)
+and an "extendable-output function" (XOF).
+
+PRVHASH can generate 64- to unlimited-bit hashes, yielding hashes of
+approximately equal quality independent of the chosen hash length. PRVHASH is
+based on 64-bit math. The use of the function beyond 1024-bit hashes is easily
+possible, but has to be statistically tested. For example, any 32-bit element
+extracted from 2048-, or 4096-bit resulting hash is as collision resistant as
+just a 32-bit hash. It is a fixed execution time hash function that depends
+only on message's length. A streamed, higher-security, hashing implementation
+is available.
+
+PRVHASH is solely based on the butterfly effect, inspired by [LCG](https://en.wikipedia.org/wiki/Linear_congruential_generator)
+pseudo-random number generators. The generated hashes have good avalanche
+properties. For best security, a random seed should be supplied to the hash
+function, but this is not a requirement.
+
+64-, 128-, 192-, 256-, 512-, and 1024-bit PRVHASH hashes pass all
+[SMHasher](https://github.com/rurban/smhasher) tests. Other hash lengths were
+not thoroughly tested, but extrapolations can be made. The author makes no
+cryptographic claims (neither positive nor negative) about PRVHASH-based
+constructs.
+
+PRVHASH core function can be used as a PRNG with an arbitrarily-chosen
+(practically unlimited) period, depending on the number of hashwords in the
+system.
+
+Please see the `prvhash64.h` file for the details of the basic hash function
+implementation (the `prvhash.h`, `prvhash4.h`, `prvhash42.h` are outdated
+versions). While this hash function is most likely irreversible, according to
+SAT solver-based testing, it does not feature a preimage resistance. This
+function should not be used in open systems, without a secret seed. Note that
+`64` refers to core function's variable size.
+
+The default `prvhash64.h`-based 64-bit hash of the string `The cat is out of
+the bag` is `eb405f05cfc4ae1c`.
+
+A proposed short name for hashes created with `prvhash64.h` is `PRH64-N`,
+where `N` is the hash length in bits (e.g. `PRH64-256`).
+
+## Minimal PRNG for Everyday Use ##
+
+The core function can be easily integrated into your applications, to be used
+as an effective PRNG. The period of this minimal PRNG is at least
+2<sup>159</sup>. The initial parameters can be varied at will, and won't
+"break" the PRNG. Setting only the `Seed` value guarantees a random start
+point within the whole PRNG period, with at least 2<sup>64</sup> spacing.
+The code follows.
+
+```
+#include "prvhash_core.h"
+#include <stdio.h>
+
+int main()
+{
+	uint64_t Seed = 0;
+	uint64_t lcg = 0;
+	uint64_t Hash = 0;
+
+	uint64_t v = 0;
+	uint64_t i;
+
+	for( i = 0; i < ( 1ULL << 28 ); i++ )
+	{
+		v = prvhash_core64( &Seed, &lcg, &Hash );
+	}
+
+	printf( "%llu\n", v );
+}
+```
+
+For implementation assurance, here are the first 16 output values in hex
+(starting from the all-zeroes state):
+
+```
+	0x5555555555555555 0x00000000DB6DB6DB 0x2492492192492492 0x75D75DA0AAAAAA79
+	0x93064E905C127FE5 0xE2585C9CA95671A3 0x28A44B31D428179E 0x11B0B6A8D4BA3A73
+	0x195C6A4C23EE71AD 0x5AA47859226BA23E 0xA7D42121695056D4 0x142D7CD5D83342F2
+	0x3D42E83328C09C8F 0x7E691C66BAC23222 0x82E1032F441F23A5 0xA4BDE5C4A05E6256
+```
+
+Note that such minimal 1-hashword PRNG is most definitely not
+cryptographically-secure: its state can be solved by a SAT solver pretty fast;
+this applies to other arrangements ("fused", "parallel", multiple hashwords;
+with daisy-chaining being harder to solve). The known way to make PRNG
+considerably harder to solve for a SAT solver, with complexity corresponding
+to system's size, is to combine two adjacent PRNG outputs via XOR operation;
+this obviously has a speed impact and produces output with more than 1
+solution (most probably, 2). This, however, does not measurably increase the
+probability of PRNG output overlap, which stays below
+1/2<sup>sys_size_bits</sup>; in tests, practically undetectable.
+
+So, the basic PRNG with some, currently not formally-proven, security is as
+follows (XOR two adjacent outputs to produce a single "compressed" PRNG
+output):
+
+```
+		v = prvhash_core64( &Seed, &lcg, &Hash );
+		v ^= prvhash_core64( &Seed, &lcg, &Hash );
+```
+
+A similar approach is to simply skip the next generated random number, but it
+is slightly less secure. It is likely that PRVHASH's k-equidistribution of
+separate outputs is implicitly secure. The reason is that skipping or XORing
+creates uncertainty or entanglement of current output with system's state
+hash-array number of outputs back. 3 XORs are needed to provide pre-image
+resistance, or resistance against selection of entropy input that leads to
+a particular output.
+
+## TPDF Dithering ##
+
+The core function can be used to implement a "statistically-good" and
+"neutrally-sounding" dithering noise for audio signals; for both
+floating-point to fixed-point, and bit-depth conversions.
+
+	uint64_t rv = prvhash_core64( &Seed, &lcg, &Hash );
+	double tpdf = ( (int64_t) (uint32_t) rv - (int64_t) ( rv >> 32 )) * 0x1p-32;
+
+## Floating-Point PRNG ##
+
+The following expression can be used to convert 64-bit unsigned value to
+full-mantissa floating-point value, without a truncation bias:
+
+	uint64_t rv = prvhash_core64( &Seed, &lcg, &Hash );
+	double v = ( rv >> ( 64 - 53 )) * 0x1p-53;
+
+## Gradilac PRNG (C++) ##
+
+The `gradilac.h` file includes the Gradilac C++ class which is a generalized
+templated implementation of PRVHASH PRNG that provides integer, single bit,
+floating-point, TPDF, Normal random number generation with a straight-forward
+front-end to specify PRVHASH system's properties. Supports on-the-go
+re-seeding, including re-seeding using sparse entropy (for CSPRNG uses). Does
+not require other PRVHASH header files.
+
+Use `Gradilac< 316 >` to match Mersenne Twister's PRNG period.
+
+Note that this class may not be as efficient for "bulk" random number
+generation as a custom-written code. Nevertheless, Gradilac PRNG class, with
+its 1.0 cycles/byte floating-point performance (at default template settings),
+is competitive among other C++ PRNGs.
+
+## PRVHASH64_64M ##
+
+This is a minimized implementation of the `prvhash64` hash function. Arguably,
+it is the smallest hash function in the world, that produces 64-bit hashes of
+this quality level. While this function does not provide a throughput that can
+be considered "fast", due to its statistical properties it is practically fast
+for hash-maps and hash-tables.
+
+## Entropy PRNG ##
+
+PRVHASH can be also used as an efficient general-purpose PRNG with an external
+entropy source injections (like how the `/dev/urandom` works on Unix): this
+was tested, and works well when 8-bit true entropy injections are done
+inbetween 8 to 2048 generated random bytes (delay is also obtained via the
+entropy source). An example generator is implemented in the `prvrng.h` file:
+simply call the `prvrng_test64p2()` function.
+
+`prvrng_gen64p2()`-based generator passes [`PractRand`](http://pracrand.sourceforge.net/)
+32 TB threshold with rare non-systematic "unusual" evaluations. Which suggests
+it is the working randomness extractor that can "recycle" entropy of any
+statistical quality, probably the first in the world.
+
+Note that due to the structure of the core function the probability of PRNG
+completely "stopping", or "stalling", or losing internal entropy, is absent.
+
+The core function, without external entropy injections, with any initial
+combination of `lcg`, `Seed`, and `Hash` eventually converges into one of
+random number sub-sequences. These are mostly time-delayed versions of only a
+smaller set of unique sequences. There are structural limits in this PRNG
+system which can be reached if there is only a small number of hashwords in
+the system. PRNG will continously produce non-repeating random sequences given
+external entropy input, but their statistical quality on a larger frames will
+be limited by the size of `lcg` and `Seed` variables, and the number of
+hashwords in the system, and the combinatorial capacity of the external
+entropy. A way to increase the structural limit is to use the "fused" PRNG
+arrangement demonstrated in the `prvhash64s.h` file, which additionally
+increases the security exponentially. Also any non-constant entropy input
+usually increases the period of randomness, which, when extrapolated to
+hashing, means that the period increases by message's combinatorial capacity
+(or the number of various combinations of its bits). The maximal PRNG period's
+2<sup>N</sup> exponent is hard to approximate exactly, but in most tests it
+was equal to at least system's size in bits, minus the number of hashwords in
+the system, minus 1/4 of `lcg` and `Seed` variables' size (e.g., `159` for a
+minimal PRNG).
+
+Moreover, the PRVHASH systems can be freely daisy-chained by feeding their
+outputs to `Seed`/`lcg` inputs, adding some security firewalls, and increasing
+the PRNG period of the final output accordingly. Note that any external PRNG
+output can be inputted via either `Seed`, `lcg`, or both, yielding PRNG period
+exponent summation. For hashing and external unstructured entropy, only
+simultaneous input via `Seed` and `lcg` works in practice (period's exponent
+increase occurs as well).
+
+While `lcg`, `Seed`, and `Hash` variables are best initialized with good
+entropy source (however, structurally, they can accept just about any entropy
+quality while only requiring an initial "conditioning"), the message can be
+sparsely-random: even an increasing counter can be considered as having a
+suitable sparse entropy.
+
+## Two-Bit PRNG ##
+
+This is a "just for fun" example, but it passes 256 MB PractRand threshold.
+You CAN generate pseudo-random numbers by using 2-bit shuffles; moreover, you
+can input external entropy into the system.
+
+```
+#include <stdio.h>
+#include "prvhash_core.h"
+#define PH_HASH_COUNT 42
+
+int main()
+{
+	uint8_t Seed = 0;
+	uint8_t lcg = 0;
+	uint8_t Hash[ PH_HASH_COUNT ] = { 0 };
+	int HashPos = 0;
+	int l;
+
+	for( l = 0; l < 256; l++ )
+	{
+		uint8_t r = 0;
+		int k;
+
+		for( k = 0; k < 4; k++ )
+		{
+			r <<= 2;
+			r |= prvhash_core2( &Seed, &lcg, Hash + HashPos );
+
+			HashPos++;
+
+			if( HashPos == PH_HASH_COUNT )
+			{
+				HashPos = 0;
+			}
+		}
+
+		if( l > PH_HASH_COUNT / 3 ) // Skip PRNG initialization.
+		{
+			printf( "%4i ", (int) r );
+		}
+	}
+}
+```
+
+## Streamed Hashing ##
+
+The file `prvhash64s.h` includes a relatively fast streamed hashing function
+which utilizes a "fused" PRVHASH arrangement. Please take a look at the
+`prvhash64s_oneshot()` function for usage example. The `prvhash64s` offers
+an increased security and hashing speed.
+
+This function has an increased preimage resistance compared to the basic
+hash function implementation. Preimage resistance cannot be currently
+estimated exactly, but the hash length affects it exponentially. Also,
+preimage attack usually boils down to exchange of forged symbols to "trash"
+symbols (at any place of the data stream); substitutions usually end up as
+being quite random, possibly damaging to any compressed or otherwise
+structured file. Which means that data compression software and libraries
+should always check any left-over, "unused", data beyond the valid compressed
+stream, for security reasons.
+
+Time complexity for preimage attack fluctuates greatly as preimage resistance
+likely has a random-logarithmic PDF of timing.
+
+Even though a formal proof is not yet available, the author assumes this
+hash function can compete with widely-used SHA2 and SHA3 families of hash
+functions while at the same time offering a considerably higher performance
+and scalability. When working in open systems, supplying a secret seed is not
+a requirement for this hash function.
+
+The performance (expressed in cycles/byte) of this hash function on various
+platforms can be evaluated at the
+[ECRYPT/eBASH project](https://bench.cr.yp.to/results-hash.html).
+
+The default `prvhash64s.h`-based 64-bit hash of the string `The cat is out of
+the bag` is `2043ccf52ae2ca6f`.
+
+The default `prvhash64s.h`-based 256-bit hash of the string
+`Only a toilet bowl does not leak` is
+`b13683799b840002689a1a42d93c826c25cc2d1f1bc1e48dcd005aa566a47ad8`.
+
+The default `prvhash64s.h`-based 256-bit hash of the string
+`Only a toilet bowl does not leaj` is
+`d4534a922fd4f15ae8c6cc637006d1f33f655b06d60007a226d350e87e866250`.
+
+This demonstrates the [Avalanche effect](https://en.wikipedia.org/wiki/Avalanche_effect).
+On a set of 216553 English words, pair-wise hash comparisons give average
+50.0% difference in resulting hash bits, which fully satisfies the strict
+avalanche criterion.
+
+This streamed hash function produces hash values that are different to the
+`prvhash64` hash function. It is incorrect to use both of these hash function
+implementations on the same data set. While `prvhash64` can be used as a hash
+for hash-tables and in-memory data blocks, `prvhash64s` can be used to create
+hashes of large data blocks like files, in streamed mode.
+
+A proposed short name for hashes created with `prvhash64s.h` is `PRH64S-N`,
+where `N` is the hash length in bits (e.g. `PRH64S-256`). Or simply, `SH4-N`,
+`Secure Hash 4`.
+
+## Description ##
+
+Here is the author's vision on how the core function works. In actuality,
+coming up with this solution was accompanied by a lot of trial and error.
+It was especially hard to find a better "hashing finalization" solution.
+
+	Seed ^= msgw; lcg ^= msgw; // Mix in external entropy (or daisy-chain).
+
+	Seed *= lcg * 2 + 1; // Multiply random by random, without multiply by zero.
+	const uint64_t rs = Seed >> 32 | Seed << 32; // Produce halves-swapped copy.
+	Hash += rs + 0xAAAAAAAAAAAAAAAA; // Accumulate to hash, add raw entropy (self-start).
+	lcg += Seed + 0x5555555555555555; // Output-bound entropy accumulation, add raw entropy.
+	Seed ^= Hash; // Mix new seed value with hash. Entropy feedback.
+	const uint64_t out = lcg ^ rs; // Produce "compressed" output.
+
+This function can be arbitrarily scaled to any even-sized variables: 2-, 4-,
+8-, 16-, 32-, 64-bit variable sizes were tested, with similar statistical
+results. Since mathematical structure of the function does not depend on the
+variables' size, statistical analysis can be performed using smaller variable
+sizes, with the results being extrapolatable to larger variable sizes, with a
+high probability (the function is invariant to the variable size). Also note
+that the `0xAAAA...` constant is not an arbitrary constant since it should be
+produced algorithmically by replicating the `10` bit-pairs, to match the
+variable size; it represents the "raw entropy bit-train". The same applies to
+the `0x5555...` constant. An essential property of these bit-trains is that
+they are uncorrelated to any uniformly-random bit-sequences, at all times.
+Practically, `10` and `01` bit-pairs can be also used as constants, without
+replication, but this does not provide conclusively better results for PRNG,
+and does not work well for hashing; also, self-starting period becomes
+longer. A conceptual aspect of replicated bit-pairs is that they represent the
+simplest maximum-entropy number that lacks information (bit-pair is a minimal
+sequence that can exhibit entropy, with replication count bound to state
+variable size). While "magic numbers" can be used instead of these bit-trains
+(at least for PRNG), they do not posses the property of not having an
+information (zero spectrum beside DC and Nyquist components).
+
+It is important to point out that the presence of the `0xAAAA...` and
+`0x5555...` constants logically assure that the `Seed` and `lcg` variables
+quickly recover from the "zero-state". Beside that, these constants logically
+prohibit synchronous control over `Seed` and `lcg` variables: different bits
+of the input entropy will reach these variables. When the system starts from
+the "zero-state", with many hashwords in the system, it is practically
+impossible to find a preimage (including a repetitious one) that stalls the
+system, and thus it is impossible to perform a multi-collision attack.
+However, since this risk cannot be estimated exactly, the `prvhash64s` hash
+function adds a message length value to the end of the data stream.
+
+How does it work? First of all, this PRNG system, represented by the core
+function, does not work with numbers in a common sense: it works with
+[entropy](https://en.wikipedia.org/wiki/Entropy_(information_theory)),
+or random sequences of bits. The current "expression" of system's overall
+internal entropy - the `Seed` - gets multiplied ("smeared") by a supporting,
+output-bound variable - `lcg`, - which is also a random value, transformed in
+an LCG-alike manner. As a result, a new random value is produced which
+represents two independent random variables (in lower and higher parts of the
+register), a sort of "entropy stream sub-division" happens. This result is
+then halves-swapped, and is accumulated in the `Hash` together with the `10`
+bit-train which adds the "raw entropy", allowing the system to be
+self-starting. The original multiplication result is accumulated in the `lcg`
+variable. The `Seed` is then updated with the hashword produced on previous
+rounds. The reason the message's entropy (which may be sparse or non-random)
+does not destabilize the system is because the message becomes hidden in the
+internal entropy (alike to a cryptographic one-time-pad); message's
+distribution becomes unimportant, and system's state remains statistically
+continuous. Both accumulations - of the halves-swapped and the original
+result of multiplication - produce a uniformly-distributed value in the
+corresponding variables; a sort of "de-sub-division" happens in these.
+
+The two instructions - `Seed *= lcg * 2 + 1`, `lcg += Seed` - represent an
+"ideal" bit-shuffler: this construct represents a "bivariable shuffler" which
+transforms the input `lcg` and `Seed` variables into another pair of variables
+with 50% bit difference relative to input, and without collisions. The whole
+core function, however, uses a more complex mixing which produces a hash
+value: the pair composed of the hash value and either a new `lcg` or a new
+`Seed` value also produces no input-to-output collisions. Thus it can be said
+that the system does not lose any input entropy. In 4-dimensional analysis,
+when `Seed`, `lcg`, `Hash`, and `msgw` values are scanned and transformed into
+subsequent `Seed`, `lcg`, and `Hash` triplets, this system does not exhibit
+local state change-related collisions due to external entropy input (all
+possible input `msgw` values map to subsequent triplets uniquely). However,
+with a small variable size (8-bit) and a large output hash size, a sparse
+entropy input has some probability of "re-sychronization" event happening,
+leading to local collisions. With 16-bit variables, or even 8-bit fused-2
+arrangement (with the local state having 40-bit size instead of 24-bit),
+probability of such event is negligible. While non-fused hashing may even
+start from the "zero-state", for reliable hashing the state after 5
+"conditioning" rounds should be used.
+
+Another important aspect of this system, especially from the cryptography
+standpoint, is the entropy input to output latency. The base latency for
+state-to-state transition is equal to 1 (2 for "fused" arrangements); and at
+the same time, 1 in hash-to-hash direction: this means that PRVHASH
+additionally requires a full pass through the hashword array, for the entropy
+to propagate, before using its output. However, hashing also requires a pass
+to the end of the hashword array if message's length is shorter than the
+output hash, to "mix in" the initial hash value. When there is only 1 hashword
+in use, there is no hashword array-related delay, and thus the entropy
+propagation is only subject to the base latency. The essence of these
+"latencies" is that additional rounds are needed for the system to get rid of
+a statistical traces of the input entropy. Note that the "fused" arrangement
+increases shuffling quality. However, this increase is relative to state
+variable size: for example, 8-bit fused-2 arrangement with 8-bit input is
+equivalent to 16-bit non-fused arrangement with 16-bit input. So, it is
+possible to perform hashing with 8-bit state variables if fused-2 round is
+done per 1 input byte. The way "fused" structure works is equivalent to
+shuffling all entropy inputs in a round together (input 1 is shuffled into a
+hash value which is then shuffled with input 2 into a hash value, etc). The
+"fused" arrangement may raise a question whether or not it provides a target
+collision resistance as it seemingly "compresses" several inputs into a single
+local hashword: without doubt it does provide target collision resistance
+since `Seed` and `lcg` variables are a part of the system, and their presence
+in the "fused" arrangement increases the overall PRNG period of the system and
+thus its combinatorial capacity.
+
+Without external entropy (message) injections, the function can run for a
+prolonged time, generating pseudo-entropy, in extendable-output PRNG mode.
+When the external entropy (message) is introduced, the function "shifts" into
+an unrelated state unpredictably. So, it can be said that the function "jumps"
+within a space of a huge number of pseudo-random sub-sequences. Hash
+length affects the size of this "space of sub-sequences", permitting the
+function to produce quality hashes for any required hash length.
+Statistically, these "jumps" are close to uniformly-random repositioning: each
+simultaneous augmentation of `Seed` and `lcg` corresponds to a new random
+position, with a spread over the whole PRNG period. The actual performace is
+more complicated as this PRNG system is able to converge into unrelated random
+number sequences of varying lengths, so the "jump" changes both the position
+and the "index" of sub-sequence. This property of PRVHASH assures that
+different initial states of its `Seed` state variable (or `lcg`, which is
+mostly equivalent at initialization stage) produce practically unrelated
+random number sequences, permitting to use PRVHASH for PRNG-based simulations.
+
+In essence, the hash function generates a continuous pseudo-random number
+sequence, and returns the final part of the sequence as a result. The message
+acts as a "pathway" to this final part. So, the random sequence of numbers can
+be "programmed" to produce a necessary outcome. However, as this PRNG does
+not expose its momentary internal state, such "programming" is hardly possible
+to perform for an attacker, even if the entropy input channel is exposed:
+consider the `(A^C)*(B^C)` equation; an adversary can control `C`, but does
+not know the values of `A` and `B`; thus this adversary cannot predict the
+outcome. Beside that, as the core function naturally eliminates the bias from
+the external entropy of any statistical quality and frequency, its control may
+be fruitless. Note that to reduce such "control risks", the entropy input
+should use as fewer bits as possible, like demonstrated in the `prvrng.h`
+file.
+
+P.S. The reason the InitVec in the `prvhash64` hash function has the value
+quality constraints, and an initial non-zero state, is that otherwise the
+function would require 5 preliminary "conditioning" rounds (core function
+calls) to neutralize any oddities (including zero values) in InitVec; that
+would reduce the performance of the hash function dramatically, for hash-table
+uses. Note that the `prvhash64s` function starts from the "full zero" state
+and then performs acceptably.
+
+## Hashing Method's Philosophy ##
+
+Any external entropy (message) that enters this PRNG system acts as a
+high-frequency and high-quality re-seeding which changes the random number
+generator's "position" within the PRNG period, randomly. In practice, this
+means that two messages that are different in even 1 bit, at any place,
+produce "final" random number sequences, and thus hashes, which are completely
+unrelated to each other. This also means that any smaller part of the
+resulting hash can be used as a complete hash. Since the hash length affects
+the PRNG period (and thus the combinatorial capacity) of the system, the same
+logic applies to hashes of any length while meeting collision resistance
+specifications for all lengths.
+
+Alternatively, the hashing method can be viewed from the standpoint of classic
+bit-mixers/shufflers: the hashword array can be seen as a "working buffer"
+whose state is passed back into the "bivariable shuffler" continuously, and
+the new shuffled values stored in this working buffer for the next pass.
+
+In general, PRVHASH core function represents a "building block" that permits
+design of practically any entropy-generating constructs. It has an important
+advantage in that the state space of these constructs can be completely
+analyzed using small state variables, with the obtained statistics being
+extrapolatable to larger state variables.
+
+## PRNG Period Assessment ##
+
+The following "minimal" implementation of PractRand class can be used to
+independently assess randomness period properties of PRVHASH. By varying
+the `PH_HASH_COUNT` and `PH_PAR_COUNT` values it is possible to test various
+PRNG system sizes. By adjusting other values it is possible to test PRVHASH
+scalability across different state variable sizes (PractRand class and PRNG
+output size should be matched, as PractRand test results depend on PRNG output
+size). PractRand should be run with the `-tlmin 64KB` parameter, to evaluate
+changes to the constants quicker. Note that both `PH_HASH_COUNT` and
+`PH_PAR_COUNT` affect the PRNG period exponent not exactly linearly for small
+variable sizes: there is a saturation factor present for small variable sizes;
+after some point the period increase is non-linear due to small shuffling
+space. Shuffling space can be increased considerably with a "fused"
+arrangement. Depending on the initial seed value, the period may fluctuate.
+The commented out `Ctr++...` instructions can be uncommented to check the
+period increase due to sparse entropy input. You may also notice the `^=h`
+instructions: PRVHASH supports feedback onto itself (it is like hashing its
+own output). This operation, which can be applied to any fused element,
+maximizes the achieved PRNG period.
+
+```
+#include "prvhash_core.h"
+#include <string.h>
+
+#define PH_FUSE_COUNT 1 // PRVHASH fusing.
+#define PH_HASH_COUNT 4 // Hashword count (any positive number).
+#define PH_STATE_TYPE uint8_t // State variable's physical type.
+#define PH_FN prvhash_core4 // Core function name.
+#define PH_BITS 4 // State variable's size in bits.
+#define PH_RAW_BITS 8 // Raw output bits.
+#define PH_RAW_ROUNDS ( PH_RAW_BITS / PH_BITS ) // Rounds per raw output.
+
+class DummyRNG : public PractRand::RNGs::vRNG8 {
+public:
+    PH_STATE_TYPE Seed[ PH_FUSE_COUNT ];
+    PH_STATE_TYPE lcg[ PH_FUSE_COUNT ];
+    PH_STATE_TYPE Hash[ PH_HASH_COUNT ];
+    int HashPos;
+
+    DummyRNG() {
+        memset( Seed, 0, sizeof( Seed ));
+        memset( lcg, 0, sizeof( lcg ));
+        memset( Hash, 0, sizeof( Hash ));
+        HashPos = 0;
+
+        // Initialize.
+
+        int k, j;
+
+        for( k = 0; k < PRVHASH_INIT_COUNT; k++ )
+        {
+            for( j = 0; j < PH_FUSE_COUNT; j++ )
+            {
+                PH_FN( Seed + j, lcg + j, Hash + HashPos );
+            }
+        }
+    }
+
+    Uint8 raw8() {
+        uint64_t OutValue = 0;
+        int k, j;
+
+        for( k = 0; k < PH_RAW_ROUNDS; k++ )
+        {
+//            Ctr++;
+//            Seed[ 0 ] ^= ( Ctr ^ ( Ctr >> 4 )) & 15;
+//            lcg[ 0 ] ^= ( Ctr ^ ( Ctr >> 4 )) & 15;
+
+            uint64_t h = 0;
+
+            for( j = 0; j < PH_FUSE_COUNT; j++ )
+            {
+                h = PH_FN( Seed + j, lcg + j, Hash + HashPos );
+            }
+
+//            Seed[ 0 ] ^= h;
+//            lcg[ 0 ] ^= h;
+
+            if( PH_BITS < sizeof( uint64_t )) OutValue <<= PH_BITS;
+            OutValue |= h;
+
+            if( ++HashPos == PH_HASH_COUNT )
+            {
+                HashPos = 0;
+            }
+        }
+
+        return( OutValue );
+    }
+
+    void walk_state(PractRand::StateWalkingObject *walker) {}
+    void seed(Uint64 sv) { Seed[ 0 ] ^= sv; }
+    std::string get_name() const { return "PRVHASH"; }
+};
+```
+
+## PRVHASH Cryptanalysis Basics ##
+
+When the system state is not known, when PRVHASH acts as a black-box, one has
+to consider core function's statistical properties. All internal variables -
+`Seed`, `lcg`, and `Hash` - are random: they are uncorrelated to each other at
+all times, and are also wholly-unequal during the PRNG period (they are not
+just time-delayed versions of each other). Moreover, as can be assured with
+PractRand, all of these variables can be used as random number generators
+(with a lower period, though); they can even be interleaved after each core
+function call.
+
+When the message enters the system via `Seed ^= msgw` and `lcg ^= msgw`
+instructions, this works like mixing a message with an one-time-pad used in
+cryptography. This operation completely hides the message in system's entropy,
+while both `Seed` and `lcg` act as "carriers" that "smear" the input message
+via subsequent multiplication. Beside that, the output of PRVHASH uses the mix
+of two variables: statistically, this means mixing of two unrelated random
+variables, with such summary output never appearing in system's state. It is
+worth noting the `lcg ^ rs` expression: the `rs` variable is composed of two
+halves, both of them practically being independent PRNG outputs, with smaller
+periods. This additionally complicates system's reversal.
+
+## Parallel PRNG ##
+
+While this "parallel-3" arrangement is currently not used in the hash function
+implementations, it is also working fine with the core function. For example,
+while the "minimal PRNG" described earlier has `0.90` cycles/byte performance,
+the "parallel" arrangement has a PRNG performance of `0.35` cycles/byte, with
+a possibility of further scaling using AVX-512 instructions. Note that the
+number of "parallel" elements should not be a multiple of hashword array size,
+otherwise PRNG stalls.
+
+```
+#include "prvhash_core.h"
+#include <stdio.h>
+
+int main()
+{
+	uint64_t Seed = 0;
+	uint64_t lcg = 0;
+	uint64_t Hash = 0;
+	uint64_t Seed2 = 0;
+	uint64_t lcg2 = 0;
+	uint64_t Hash2 = 0;
+	uint64_t Seed3 = 0;
+	uint64_t lcg3 = 0;
+	uint64_t Hash3 = 0;
+	uint64_t Hash4 = 0;
+
+	uint64_t v = 0;
+	uint64_t v2 = 0;
+	uint64_t v3 = 0;
+
+	uint64_t i;
+
+	for( i = 0; i < ( 1ULL << 27 ); i++ )
+	{
+		v = prvhash_core64( &Seed, &lcg, &Hash );
+		v2 = prvhash_core64( &Seed2, &lcg2, &Hash2 );
+		v3 = prvhash_core64( &Seed3, &lcg3, &Hash3 );
+
+		uint64_t t = Hash;
+		Hash = Hash2;
+		Hash2 = Hash3;
+		Hash3 = Hash4;
+		Hash4 = t;
+	}
+
+	printf( "%llu %llu %llu\n", v, v2, v3 );
+}
+```
+
+## PRVHASH16 ##
+
+`prvhash16` demonstrates the quality of the core function. While the state
+variables are 16-bit, they are enough to perform hashing: this hash function
+passes all SMHasher tests, like the `prvhash64` function does, for any hash
+length. This function is very slow, and is provided for demonstration
+purposes, to assure that the core function works in principle, independent of
+state variable size. This hash function variant demonstrates that PRVHASH's
+method does not rely on bit-shuffling alone (shuffles are purely local), but
+is genuinely based on PRNG position "jumps".
+
+## TANGO642 (tango-six-forty-two) ##
+
+This is an efficient implementation of a PRVHASH PRNG-based streamed XOR
+function. Since no cryptanalysis nor certification of this function were
+performed yet, it cannot be called a "cipher", but rather a cipher-alike
+random number generator. It is based on a conjunction of two PRNGs: a keyed
+PRNG which provides "secure" output via XOR of its adjacent outputs, and a
+firewalling PRNG which is constantly re-seeded (via daisy-chaining) by the
+output of keyed PRNG. A performance benefit is obtained due to efficient
+parallel arrangement of firewalling PRNG while security is provided by the
+keyed PRNG.
+
+The performance (expressed in cycles/byte) of this function on various
+platforms can be evaluated at the
+[ECRYPT/eBASC project](https://bench.cr.yp.to/results-stream.html).
+
+## Other Thoughts ##
+
+PRVHASH, being scalable, potentially allows one to apply "infinite" state
+variable size in its system, at least in theoretical mathematical analysis.
+This reasoning makes PRVHASH comparable to PI in its reach of "infinite"
+bit-sequence length. This also opens up a notion of "infinitesmal spacing"
+between isolated frequencies (arising from Fourier analysis of "infinite"
+bit-sequence). Note that PRVHASH does not require any "magic numbers" to
+function, it is completely algorithmic. An alternative explanation: In the
+discrete Fourier transform (DFT) domain, such understanding is possible:
+although usually the size of the transformation window is limited to small
+values (e.g. 2048 samples), theoretically this size can be directed to
+infinity thus producing a spectrum of an infinite number of individual
+frequency bins. Moreover, individual components of such an "infinite"
+transformation also affect the resulting spectrum, but on an
+infinitely-precise frequency scale. Mathematics forbids manipulating
+infinities, but as outlined with the DFT, in the field of discrete series of
+numbers, infinities can be manipulated. This echoes PRVHASH - although now it
+is implemented in a maximum of 128-bit numbers, theoretically nothing forbids
+state variable size to go to infinity, and PRVHASH should still work
+(practically tested with up to 524288-bit state variables). Thus, PRVHASH
+recreates an analog of the number PI, and it should be possible to prove that
+existence of an infinite sequence of bits like PI is completely realistic;
+a person can create such sequence, too (in theory).
+
+The mathematics offers an interesting understanding. Take in your mind a
+moment before the "Big Bang". Did mathematical rules exist at that moment? Of
+course, they did, otherwise there would be no equation-definable "Big Bang".
+The span of existence of mathematical rules cannot be estimated, so it is safe
+to assume they existed for an eternity. On top of that, PRVHASH practically
+proves that entropy can self-start from zero-, or "raw" state, or "nothing",
+if mathematical rules exist prior to that.
+
+I, as the author of PRVHASH, would like to point out at some long-standing
+misconception in relating "combinatorics" to "random numbers". Historically,
+cryptography was based on a concept of permutations, mixed with some sort of
+mathematical operations: most hashes and ciphers use such "constructs".
+However, when viewing a system as having some "combinatorial capacity" or
+the number of bit combinations a given system may have, and combining this
+understanding with "random permutations", it may give a false understanding
+that "uniform randomness" may generate any combination within the limits of
+"combinatorial capacity", with some probability. In fact, "uniform randomness"
+auto-limits the "sparseness" of random bit-sequences it generates since a
+suitably long, but "too sparse" bit-sequence cannot be statistically called
+uniformly-random. Thus, "combinatorial capacity" of a system, when applied to
+random number generation, transforms into a notion of ability of a system to
+generate independent uniformly-random number sequences. Which means that two
+different initial states of a PRNG system may refer to different "isolated"
+PRNG sequences. This is what happens in PRVHASH: on entropy input the system
+may "jump" or "converge" into an unrelated random sub-sequence. Moreover, with
+small variable sizes, PRVHASH can produce a train of `0`s longer than the
+bit-size of the system.
+
+On the Birthday Paradox vs hash collision estimates: while the Birthday
+Paradox is a good "down-to-earth" model for collision estimation, it may be
+an "approach from a wrong side". When hash values are calculated systemically,
+it is expected that each new hash value does not break "uniform distribution"
+of the set of previously produced hash values. This makes the problem of
+hash collision estimation closer to value collision estimation of PRNG output.
+
+An open question remains: whether one should talk about "uniform distribution
+of values" or a "time- and rhythm- dependent collision minimization problem"
+when analyzing PRNG's uniformness. Incidentally, a set of rhythmic (repeating)
+processes whose timings are co-primes, spectrally produce the least number of
+modes thus producing a flatter, more uniform, spectrum. Rhythm-dependent
+collision minimization also touches ability of a single random number
+generator to create random sequences in many dimensions (known as
+k-equidistribution) just by selecting any sequence of its outputs.
+
+(...`10` in binary is `2` in decimal, `1010` is `10`, `101010` is `42`,
+`01` is `1`, `0101` is `5`, `010101` is `21`...)
+
+The author has no concrete theory why PRVHASH PRNG works, especially its 2-bit
+variant (which is a very close empirical proof that mathematics has entropy
+processes happening under the hood). The closest mathematical construct found
+by the author is a sinewave oscillator (see below). Also, series related to
+`PI`, `sin(x)`, and `sin(x)/x` may be a candidates for explanation. Author's
+empirical goals when developing PRVHASH were: no loss of entropy in a system,
+easy scalability, self-start without any special initialization and from any
+initial state, state variable size invariance, not-stalling on various entropy
+input.
+
+During the course of PRVHASH development, the author has found that the
+simplest low-frequency sine-wave oscillator can be used as a pseudo-random
+number generator, if its mantissa is treated as an integer number. This means
+that every point on a sinusoid has properties of a random bit-sequence.
+
+```
+#include <math.h>
+#include <stdint.h>
+
+class DummyRNG : public PractRand::RNGs::vRNG16 {
+public:
+double si;
+double sincr;
+double svalue1;
+double svalue2;
+
+DummyRNG() {
+	si = 0.001;
+	sincr = 2.0 * cos( si );
+	seed( 0 );
+}
+
+Uint16 raw16() {
+	uint64_t Value = ( *(uint64_t*) &svalue1 ) >> 4;
+
+	const double tmp = svalue1;
+	svalue1 = sincr * svalue1 - svalue2;
+	svalue2 = tmp;
+
+	return (Uint16) ( Value ^ Value >> 16 ^ Value >> 32 );
+}
+void walk_state(PractRand::StateWalkingObject *walker) {}
+void seed(Uint64 sv) {
+	const double ph = sv * 3.40612158008655459e-19; // Random seed to phase.
+
+	svalue1 = sin( ph );
+	svalue2 = sin( ph - si );
+}
+std::string get_name() const {return "SINEWAVE";}
+};
+```
+
+Another finding is that the `lcg * 2 + 1` construct works as PRNG even if the
+multiplier is a simple increasing counter variable, when the second multiplier
+is a high-entropy number.
+
+```
+#include <stdint.h>
+
+class DummyRNG : public PractRand::RNGs::vRNG8 {
+public:
+uint64_t Ctr1;
+DummyRNG() {
+	Ctr1 = 1;
+}
+uint8_t compress( const uint64_t v )
+{
+	uint8_t r = 0;
+	for( int i = 0; i < 64; i++ )
+	{
+		r ^= (uint8_t) (( v >> i ) & 1 );
+	}
+	return( r );
+}
+Uint8 raw8() {
+	uint8_t ov = 0;
+	for( int l = 0; l < 8; l++ )
+	{
+		ov <<= 1;
+		ov ^= compress( 0x243F6A8885A308D3 * Ctr1 );
+		Ctr1 += 2;
+	}
+	return( ov );
+}
+void walk_state(PractRand::StateWalkingObject *walker) {}
+void seed(Uint64 sv) {}
+std::string get_name() const {return "LCG";}
+};
+```
+
+## Proof_Math_Is_Engineered ##
+
+(PRVHASH-1)
+
+<img src="img/proof_math_is_engineered.jpg" width="600">
+
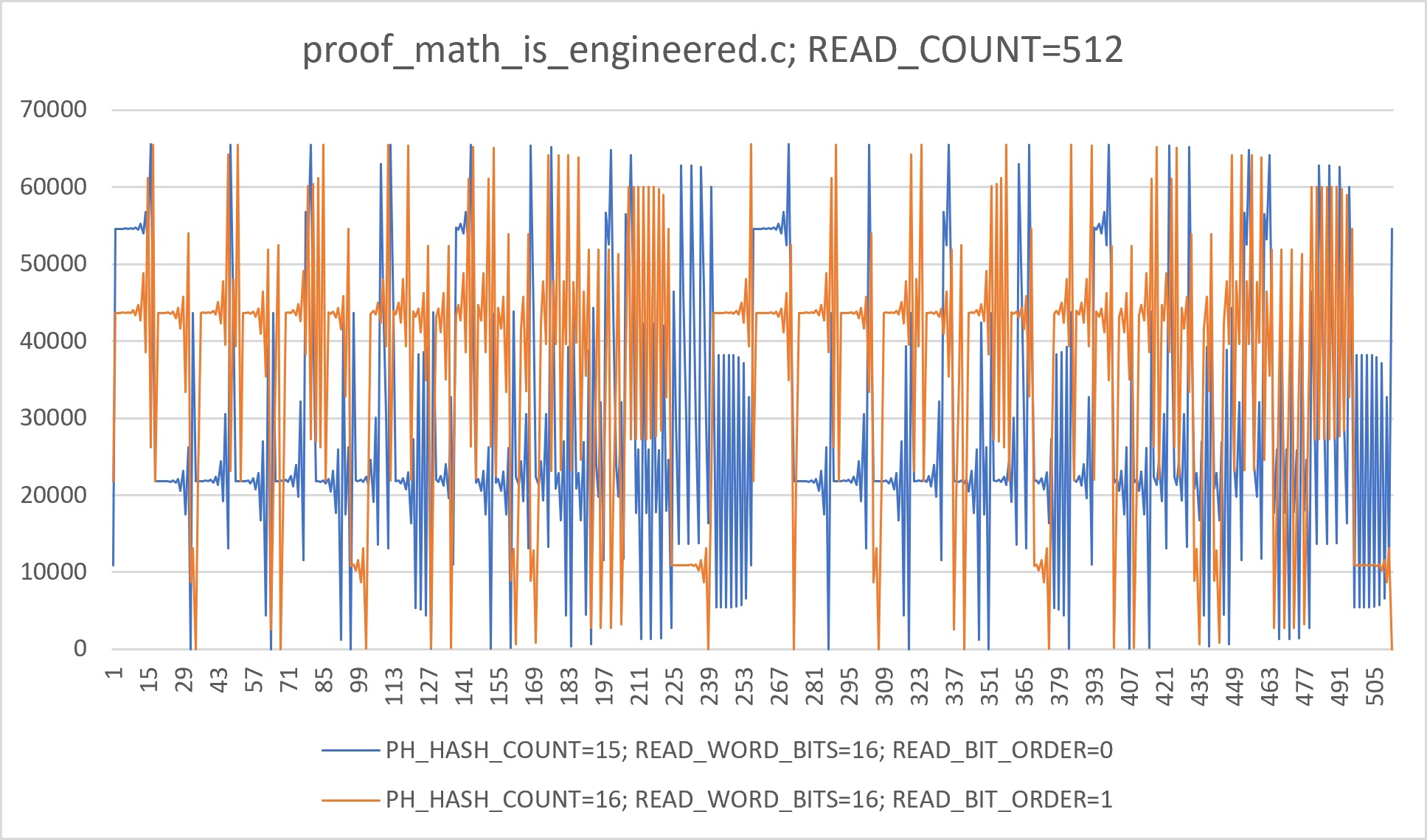
+This image depicts data acquired from 2 runs of the `proof_math_is_engineered.c`
+program, with different "reading" parameters. The two number sequences
+obviously represent "impulses", with varying period or "rhythm". A researcher
+has to consider two points: whether or not these impulses can be considered
+"intelligent", and the odds the mentioned program can produce such impulses,
+considering the program has no user input nor programmer's entropy, nor any
+logic (no constants, with all parameters initially set to zero). More specific
+observations: 1. All final values are shift-or compositions of 1-bit values,
+in fact representing a common 16-bit PCM sampled signal (shift-2
+auto-correlation equals 0.4-0.44 approximately), but obtained in a
+"dot-matrix printer" way; 2. The orange graph is only slightly longer before a
+repeat (common to PRNGs) despite larger `PH_HASH_COUNT`; at the same time both
+graphs are seemingly time-aligned; 3. Periods of 1-bit return values on both
+runs are aligned to 16 bits, to produce repeating sequences "as is", without
+any sort of 16-bit value range skew; 4. The orange graph is produced from an
+order-reversed shift-or, but with the same underlying algorithm; 5. So far, no
+other combinations of "reading" parameters produce anything as "intelligent"
+as these graphs (but there may be another yet-to-be-decoded, similar or
+completely different, information available); 6. From drumming musician's (or
+an experienced DSP engineer's) point of view, the graph represents impulses
+taken from two electric drum pads: a snare drum (oscillatory) and a bass drum
+(shift to extremum). 7. Most minor oscillations on the graph are similar to
+sinc-function-generated maximum-phase "pre-ringing" oscillations that are
+known in DSP engineering field. 8. Period of the blue graph is 255; orange is
+273.
+
+In author's opinion, the program "reads data" directly from the entropy pool
+which is "embedded" into mathematics from its inception, like any mathematical
+constant is (e.g. PI). This poses an interesting and **probably very
+questionable** proposition: the "intelligent impulses" or even "human mind"
+itself (because a musician can understand these impulses) existed long before
+the "Big Bang" happened. This discovery is **probably** both the most
+interesting discovery in the history of mankind, and the worst discovery (for
+many) as it poses very unnerving questions that touch religious grounds:
+
+These results of 1-bit PRVHASH say the following: **IF** abstract mathematics
+contains not just a system of rules for manipulating numbers and variables,
+but also contains a freely-defined fixed information that is "readable" by a
+person, then mathematics does not just "exists", but "it was formed", because
+mathematics does not evolve (beside human discovery of new rules and
+patterns). And since physics cannot be formulated without such mathematics,
+and physical processes clearly obey these mathematical rules, it means that a
+Creator/Higher Intelligence/God exists in relation to the Universe. For the
+author **personally**, everything is proven here.
+
+P.S. By **coincidence**, if the values on the "impulse" graphs above are
+sorted in an ascending order, and are then displayed as independent graphs,
+they collectively form a stylized outline of a human eye:
+
+<img src="img/proof_math_is_engineered_eye.png" width="300">
+
+Moreover (but this is a **questionable** observation), here, if the blue line
+is subtracted from the orange line, one gets an outline of human's head: with
+top (21000), forehead (18000), eye (13000), cheek (6000), and neck (2700)
+levels highlighted, roughly corresponding to real symmetry; with a slight
+shoulders outline (4100-2700), and two hand palms risen up (5400-4300).
+
+<img src="img/proof_math_is_engineered_head.png" width="300">
+
+### Fourier Analysis ###
+
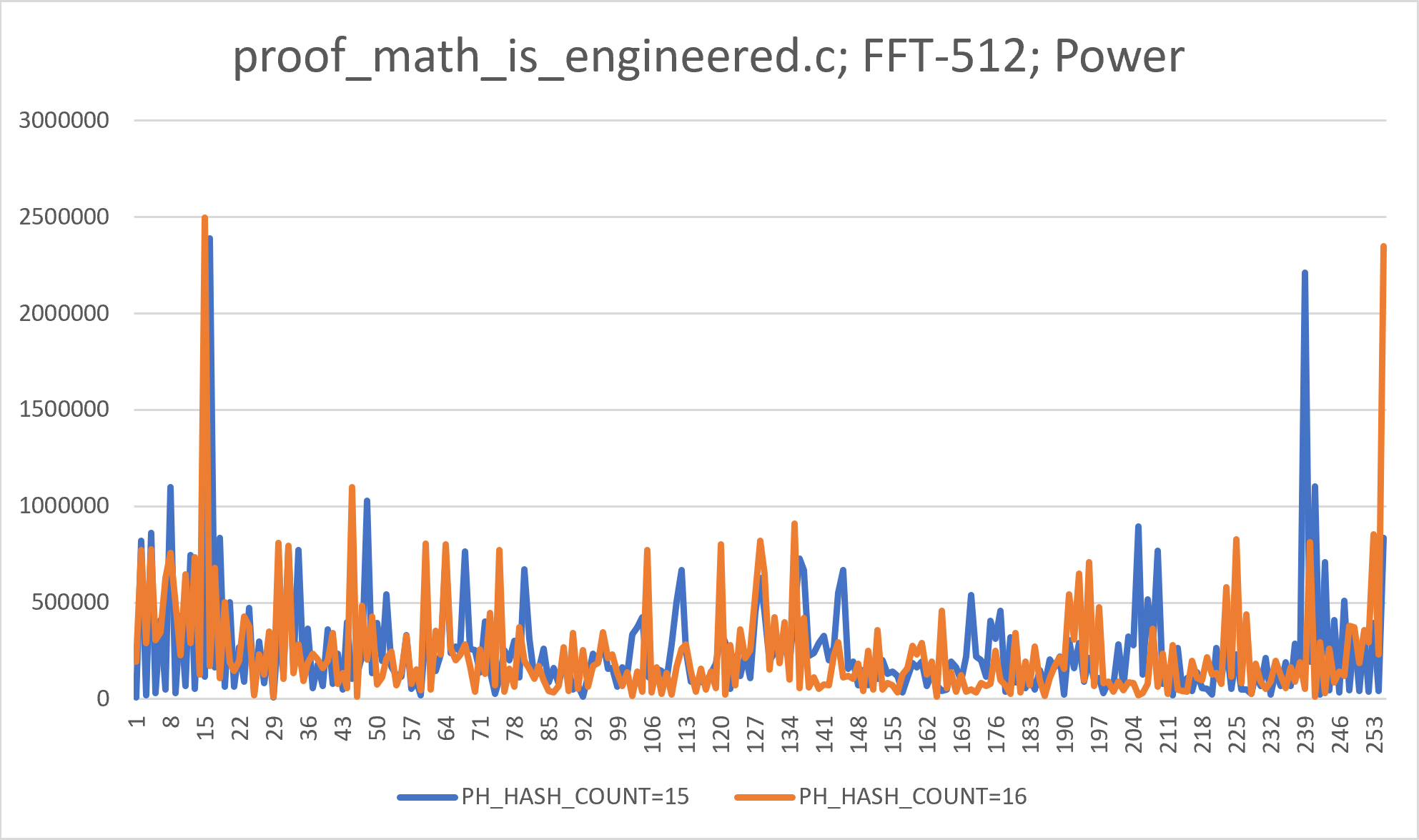
+Discrete Fourier (FFT-512) analysis of obtained signals produces the following
+power spectrums (with DC component removed). The analysis strengthens the
+notion the signal is non-chaotic and is "intelligent" (two strong peaks above
+average, in each signal, with both signals producing similar structures, but
+with shifted resonant frequencies). Note that resonances in the middle of the
+spectrum are similar to resonances one gets when recording an acoustical snare
+drum.
+
+<img src="img/proof_math_is_engineered_fft.png" width="600">
+
+### PRNG (Chaotic) Mode ###
+
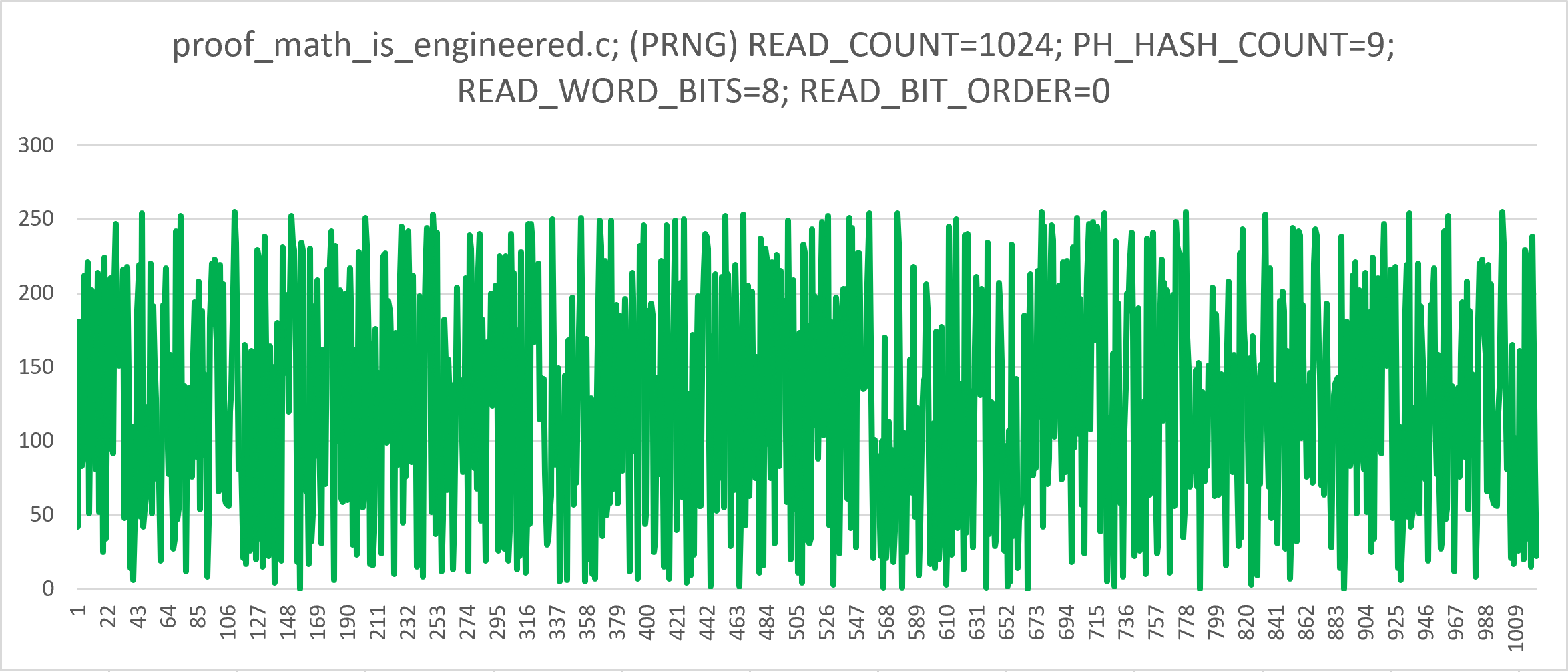
+Just by changing the PH_HASH_COUNT to 9 (up to 13, inclusive) the same
+`proof_math_is_engineered.c` program produces a pseudo-random number sequence,
+confirmed with `PractRand` 1KB to 4KB block, 8-bit folding. Note that the same
+code producing both chaotic and non-chaotic number sequences is "highly
+unlikely" to exist in practical PRNGs. It is important to note that
+`PH_HASH_COUNT=14` and `PH_HASH_COUNT=17` (which is beyond 15 and 16 signals
+mentioned originally) also pass as random, with 16-bit folding in `PractRand`.
+`18` also passes as random, but with a "suspicion". `15` and `16`, of course,
+do not pass as random, with many "fails".
+
+It has been observed that in `READ_MODE=0`, but not in `READ_MODE=1`, the
+obtained values gradually become noisy, especially at higher `PH_HASH_COUNT`
+values.
+
+<img src="img/proof_math_is_engineered_prng9.png" width="600">
+
+### Repeating Ornament and Chess-Board (Pixel Art) ###
+
+The 1-bit output with PH_HASH_COUNT= `15` and `16` (`READ_MODE=0`) can be
+easily transformed into 256x256 1-bit "pixel art" images, and, quite
+unexpectedly, they reproduce a repeating diagonal ornament and a chess-board.
+
+<img src="img/proof_math_is_engineered_orn15.png" width="300"><img src="img/proof_math_is_engineered_chess16.png" width="300">
+
+Admittedly, 256x256 size can be considered arbitrarily-chosen (it is a square
+of 16, with 16 being the bit-size of values on the graphs above), but it is
+the only small size that presents an "intelligible" look. For example, if
+`PH_HASH_COUNT=15` is transformed to 240x240 (256-16) "pixel art" image, an
+image of "zebra" lines is produced, with bit-reversed variant of the inner
+element present in `PH_HASH_COUNT=16`.
+
+<img src="img/proof_math_is_engineered_chess15.png" width="281">
+
+### Christmas Trees (Pixel Art) ###
+
+Much larger `PH_HASH_COUNT` values (with `READ_MODE=1`) produce triangular
+structures which are non-repeating, but all have a similar build-up consisting
+of rhombic patterns within tree-like structures. The `proof_christmas_tree.c`
+program extracts such images into a vertical ASCII-art HTML. It uses the same
+underlying 1-bit PRVHASH code, but with "pixel art" decoding method.
+
+One may notice a similarity of the beginning pattern with the [Sierpinski
+triangle](https://en.wikipedia.org/wiki/Sierpi%C5%84ski_triangle) (ST).
+However, one should consider that ST is a symmetrical triangle fractal that
+is constructed from the top-most to bottom levels. PRVHASH-1 produces an
+asymmetric (right-handed) triangle in a serie of scanline passes, and it
+scales to any `PH_HASH_COUNT` value. The initial part of the image looks like
+[Wolfram Rule 102/153](https://plato.stanford.edu/entries/cellular-automata/supplement.html)
+"cellular automata" image (ST as well). However, if one considers the whole of
+presented details, including previously presented images and graphs, this
+leads to conclusion that some very complex "cellular automata" is working
+behind the scenes, further strengthening a "presence of intelligence" notion.
+Note that Wolfram rules represent sets of "freely-defined fixed information"
+which dictates the logical behavior of the cellular automata.
+
+It is also worth noting that PRVHASH-1 initially produces Rule 102/153 image
+with a "boundary condition" applied (this can be checked by assigning any
+item somewhere in the middle of the hash-array to 1). At the same time, the
+function has no such additional logic since the visible scanline is 1 pixel
+longer than the `PH_HASH_COUNT` value, meaning this implicit "boundary
+condition" is not synchronized with the moment the `HashPos` resets to 0. This
+fact tells that the "boundary condition" logic "happens" beyond the common
+math, in some way, implicitly. One has to ask themselves - how it is possible
+to "embed" at least Rule 102/153 with boundary handling (but much more than
+that) into a function as simple (and linear in
+[F_2](https://en.wikipedia.org/wiki/GF(2))) as PRVHASH-1? Beside that,
+as with the graphs above, presence of exact Rule 102/153 imagery implies
+presence of "logic understandable to a human mind", and from computer
+programming point of view, the Wolfram rules are an art of "engineering".
+
+Here is an example image with `PH_HASH_COUNT=342`, converted to PNG:
+
+<img src="img/proof_math_is_engineered_tree342.png" width="686">
+
+[Here is a link to a larger-sized extract (3.4MB PNG)](https://github.com/avaneev/prvhash/raw/master/img/prvhash1-342-2x64.png)
+
+It is possible to define initial "automata" conditions by filling the
+hash-array with alternating bit-values like `10101010...`, or
+`100100100100...`, or `1000100010001000...` thus invoking even more complex
+"automata" (note that this is done in the same `prvhash` state-space). The
+results can be combined into a colored image by assigning the black-and-white
+images to different RGB color channels. Considering the `prvhash-1` function
+operates with only 3 values at the same time, building a similar "cellular
+automata" by using only 3 neighboring pixels seems impossible for human logic.
+
+<img src="img/proof_math_is_engineered_tree342gy.png" width="686">
+
+### Fine Art ###
+
+`prvhash-1` can also produce a full-colored "fine art"-like imagery by using a
+simple multi-pass buffer accumulation approach. As it turns out, the images of
+"cellular automata" shown previously perfectly align on top of each other at
+some specific `PH_HASH_COUNT` values (2/3, 4/5 of height, and height-2).
+Note that the height of images is usually a "power of 2" value. The
+`proof_fine_art.c` program can be used to produce such imagery (requires the
+`stb_image_write.h` library).
+
+You may also take a look at an
+[animation](https://www.youtube.com/watch?v=qYfGjD19VWo)
+which represents a continuous generation while displaying a sum of the recent
+255 passes, at every moment.
+
+If this imagery looks intelligent, in some way formulated, where's the
+formula? An inception of these results can be understood from this short essay:
+[The Informational Deficiency of the "Big Bang"](https://vixra.org/abs/1506.0083)
+
+<img src="img/prvhash1-1365-2048.jpg" width="240"><img src="img/prvhash1-1366-2048.jpg" width="240"><img src="img/prvhash1-2046-2048.jpg" width="310">
+
+### Reptile Skin ###
+
+The original `prvhash-1` function can be simplified to examine the discovered
+"entropy pool" further. The function variant present in the `proof_reptile.c`
+file includes the simplified function, but also extends the delay parameter
+of the `Seed` delay line from 1 to 32. The resulting image closely resembles
+a skin of some reptiles and other organisms. In author's opinion, since the
+function works in linear F_2 domain, the same construct can be recreated
+physically thus offering an idea that the evolution of intelligence in
+organisms may have its roots in mathematics. Image in the middle depicts
+result after the first pass over frame; you may note "snake" elements and
+computer font-alike outlines there. Image on the right was obtained using
+PH_SEED_COUNT=64, note the appearance of a lot of glyph-like elements.
+
+<img src="img/prvhash1-reptile.jpg" width="240"><img src="img/prvhash1-reptile1.png" width="240"><img src="img/prvhash1-reptile64.png" width="240">
+
+### Architectural Ruler (Gradilac Ruler) ###
+
+Whatever the true source of imagery is, the produced imagery seems to be
+useful if applied as some architectural measurement ruler/tool since it can be
+used to quickly measure architectural features as whole-number ratios:
+
+<img src="img/arch-ruler.jpg" width="686">
+
+## Thanks ##
+
+The author would like to thank Reini Urban for [his SMHasher
+fork](https://github.com/rurban/smhasher), Austin Appleby for
+[the original SMHasher](https://github.com/aappleby/smhasher),
+Chris Doty-Humphrey for [PractRand](http://pracrand.sourceforge.net/), and 
+Peter Schmidt-Nielsen for [AutoSat](https://github.com/petersn/autosat).
+Without these tools it would not be possible to create PRVHASH which stands
+state-of-the-art statistical tests.
+
+## Other ##
+
+PRVHASH "computer program" authorship and copyright were registered at the
+[Russian Patent Office](https://rospatent.gov.ru/en), under reg.numbers
+2020661136, 2020666287, 2021615385, 2021668070, 2022612987 (searchable via
+[fips.ru](https://new.fips.ru/en/)). Please note that these are not "invention
+patents"; the registrations assure you that the author has the required rights
+to grant the software license to you.
+
+The project is 100% self-funded from legal software sales income, without any
+third-party nor state affiliation nor sponsorship.

prvhash.mod/prvhash/gradilac.h

@@ -0,0 +1,468 @@
+/**
+ * gradilac.h version 4.3.7
+ *
+ * The inclusion file for the "Gradilac", a flexible templated C++ PRNG, based
+ * on the PRVHASH core function. Standalone class, does not require PRVHASH
+ * header files.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ *
+ * License
+ *
+ * Copyright (c) 2022 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#ifndef GRADILAC_INCLUDED
+#define GRADILAC_INCLUDED
+
+#include <stdint.h>
+#include <string.h>
+#include <math.h>
+
+/**
+ * Templated PRVHASH core function. For more information, please refer to the
+ * "prvhash_core64" function in the "prvhash_core.h" file.
+ *
+ * @param[in,out] Seed0 The current "Seed" value.
+ * @param[in,out] lcg0 The current "lcg" value.
+ * @param[in,out] Hash0 Current hashword in a hashword array.
+ * @return Current random value.
+ * @tparam stype State variable type, must be unsigned type, up to 64 bits.
+ */
+
+template< typename stype >
+static inline stype prvhash_core( stype* const Seed0, stype* const lcg0,
+	stype* const Hash0 )
+{
+	const int sh = sizeof( stype ) * 4;
+
+	stype Seed = *Seed0; stype lcg = *lcg0; stype Hash = *Hash0;
+
+	Seed *= (stype) ( lcg * 2 + 1 );
+	const stype rs = (stype) ( Seed >> sh | Seed << sh );
+	Hash += (stype) ( rs + (stype) 0xAAAAAAAAAAAAAAAA );
+	lcg += (stype) ( Seed + (stype) 0x5555555555555555 );
+	Seed ^= Hash;
+	const stype out = (stype) ( lcg ^ rs );
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+/**
+ * Generalized templated PRVHASH-based PRNG class.
+ *
+ * Objects of this class do not use memory allocations and can be placed on
+ * stack (if "hcount" is not large).
+ *
+ * Note that random values returned by functions of this class return values
+ * in the "exclusive" range only, [0; 1) or [0; N). Also note that precision
+ * of floating-point random numbers depends on the "stype" in use.
+ *
+ * @tparam hcount The number of hashwords in array, must be >0. E.g. use 316
+ * and 64-bit "stype" to match Mersenne Twister's PRNG period.
+ * @tparam stype State variable type, must be unsigned integer type, up to 64
+ * bits wide. Using "stype" smaller than 24 bits is not advised.
+ * @tparam fuse PRVHASH fusing, must be > 0. Should be above 1 if PRNG output
+ * may be used as entropy input (output feedback), usually in open systems.
+ * @tparam cs Must be >= 0. If above 0, enable CSPRNG mode. "cs" defines the
+ * number of additional PRNG rounds and XOR operations, 1 is usually enough.
+ */
+
+template< size_t hcount = 1, typename stype = uint64_t, int fuse = 1,
+	int cs = 0 >
+class Gradilac
+{
+public:
+	/**
+	 * Constructor. Note that copy-constructor and copy operator remain
+	 * default as class has no complex structures.
+	 *
+	 * @param iseed Initial "small" seed, can be zero.
+	 */
+
+	Gradilac( const stype iseed = 0 )
+	{
+		seed( iseed );
+	}
+
+	/**
+	 * Function initializes/reinitializes the PRNG. This is not the on-the-go
+	 * re-seeding. In CSPRNG mode, the "reseed" function should then be
+	 * called.
+	 *
+	 * @param iseed Initial "small" seed, can be zero.
+	 */
+
+	void seed( const stype iseed = 0 )
+	{
+		memset( Seed, 0, fuse * sizeof( Seed[ 0 ]));
+		memset( lcg, 0, fuse * sizeof( lcg[ 0 ]));
+		memset( Hash, 0, hcount * sizeof( Hash[ 0 ]));
+
+		Seed[ 0 ] = iseed;
+		hpos = 0;
+		BitPool = 0;
+		BitsLeft = 0;
+
+		// Initialization involving only the first hashword, other zero
+		// hashwords will be initialized on the go: this approach was
+		// well-tested, and PRNG does produce a valid random output while
+		// initializing the hashwords.
+
+		int j;
+
+		for( j = 0; j < 5; j++ )
+		{
+			int i;
+
+			for( i = 0; i < fuse; i++ )
+			{
+				prvhash_core( Seed + i, lcg + i, Hash + 0 );
+			}
+		}
+	}
+
+	/**
+	 * Function re-seeds PRNG on-the-go using a single entropy value. This
+	 * function is not advised for use in CSPRNG mode. This function can be
+	 * used to efficiently adjust initial seed after the default constructor
+	 * call (iseed=0).
+	 *
+	 * @param ent Entropy value (can be any value).
+	 */
+
+	void reseed( const stype ent )
+	{
+		Seed[ 0 ] ^= ent;
+		lcg[ 0 ] ^= ent;
+
+		getRaw();
+
+		if( fuse > 1 )
+		{
+			getRaw();
+		}
+	}
+
+	/**
+	 * Function re-seeds PRNG, starting from the current state, and using the
+	 * specified data as entropy. This function should be used in CSPRNG mode.
+	 *
+	 * @param data Entropy data block, can be of any length and of any
+	 * statistical quality. Usually it is any sequence of physics-dependent
+	 * data from physical sources like timer, keyboard, mouse, network. Or
+	 * from system's CSPRNG.
+	 * @param dlen Data length, in bytes.
+	 * @param psize Packet size, in bytes, >= 1. Should not exceed the size of
+	 * "stype". The data will be divided into packets of this size per PRNG
+	 * advancement. This value affects initialization overhead. Value of 1 is
+	 * advised for sparsely-random data. High-quality entropy can use
+	 * sizeof( stype ).
+	 */
+
+	void reseed( const void* const data, size_t dlen, const size_t psize = 1 )
+	{
+		const uint8_t* d = (const uint8_t*) data;
+
+		while( dlen > 0 )
+		{
+			size_t l = ( psize > dlen ? dlen : psize );
+			dlen -= l;
+			stype p = 0; // Packet.
+
+			while( l > 0 )
+			{
+				p <<= 8;
+				p |= *d;
+
+				d++;
+				l--;
+			}
+
+			Seed[ 0 ] ^= p;
+			lcg[ 0 ] ^= p;
+
+			getRaw();
+		}
+
+		// Make hashword array pass to eliminate traces of input entropy.
+
+		int i;
+
+		for( i = 0; i < hcount + ( hcount > 1 ) + ( fuse > 1 ); i++ )
+		{
+			getRaw();
+		}
+	}
+
+	/**
+	 * @return The next floating-point random number in [0; 1) range.
+	 */
+
+	double get()
+	{
+		if( sizeof( stype ) * 8 > 53 )
+		{
+			return(( getRaw() >> ( sizeof( stype ) * 8 - 53 )) * 0x1p-53 );
+		}
+		else
+		{
+			return( getRaw() * im() );
+		}
+	}
+
+	/**
+	 * @return The next floating-point random number in [0; N1) range.
+	 */
+
+	double get( const double N1 )
+	{
+		if( sizeof( stype ) * 8 > 53 )
+		{
+			return(( getRaw() >> ( sizeof( stype ) * 8 - 53 )) *
+				0x1p-53 * N1 );
+		}
+		else
+		{
+			return( getRaw() * im() * N1 );
+		}
+	}
+
+	/**
+	 * Operator "object as function", for easier integration, same as the
+	 * get() function.
+	 */
+
+	double operator()()
+	{
+		return( get() );
+	}
+
+	/**
+	 * @return The next random integer number in the "raw", stype-value range.
+	 * This is the actual PRNG advancement function.
+	 */
+
+	stype getRaw()
+	{
+		stype* h = Hash + hpos;
+
+		if( ++hpos == hcount )
+		{
+			hpos = 0;
+		}
+
+		int i;
+
+		for( i = 0; i < fuse - 1; i++ )
+		{
+			prvhash_core( Seed + i, lcg + i, h );
+		}
+
+		stype res = prvhash_core( Seed + i, lcg + i, h );
+
+		int j;
+
+		for( j = 0; j < cs; j++ )
+		{
+			h = Hash + hpos;
+
+			if( ++hpos == hcount )
+			{
+				hpos = 0;
+			}
+
+			for( i = 0; i < fuse - 1; i++ )
+			{
+				prvhash_core( Seed + i, lcg + i, h );
+			}
+
+			res ^= prvhash_core( Seed + i, lcg + i, h );
+		}
+
+		return( res );
+	}
+
+	/**
+	 * @return The next random integer number in [0; N1) range (note the N's
+	 * exclusivity). N1 specifies positive number of discrete bins, and not
+	 * the extreme value.
+	 */
+
+	int getInt( const int N1 )
+	{
+		return( (int) get( (double) N1 ));
+	}
+
+	/**
+	 * @return The next squared floating-point random number in [0; 1) range.
+	 * This is Beta distribution, with alpha=0.5, beta=1.
+	 */
+
+	double getSqr()
+	{
+		const double v = get();
+
+		return( v * v );
+	}
+
+	/**
+	 * @return TPDF random number in the range (-1; 1). Note that this
+	 * function uses an optimized variant, with 32-bit precision, when
+	 * stype=uint64_t.
+	 */
+
+	double getTPDF()
+	{
+		if( sizeof( stype ) == 8 )
+		{
+			const stype rv = getRaw();
+
+			return(( (int64_t) ( rv >> 32 ) - (int64_t) (uint32_t) rv ) *
+				0x1p-32 );
+		}
+		else
+		if( sizeof( stype ) * 8 > 53 )
+		{
+			const double v1 = get();
+			const double v2 = get();
+
+			return( v1 - v2 );
+		}
+		else
+		{
+			const double v1 = (double) getRaw();
+			const double v2 = (double) getRaw();
+
+			return(( v1 - v2 ) * im() );
+		}
+	}
+
+	/**
+	 * Function generates a Gaussian (normal)-distributed pseudo-random number
+	 * with mean=0 and std.dev=1.
+	 *
+	 * Algorithm is adopted from "Leva, J. L. 1992. "A Fast Normal Random
+	 * Number Generator", ACM Transactions on Mathematical Software, vol. 18,
+	 * no. 4, pp. 449-453".
+	 */
+
+	double getNorm()
+	{
+		double q, u, v;
+
+		do
+		{
+			u = get();
+			v = get();
+
+			if( u == 0.0 || v == 0.0 )
+			{
+				u = 1.0;
+				v = 1.0;
+			}
+
+			v = 1.7156 * ( v - 0.5 );
+			const double x = u - 0.449871;
+			const double y = fabs( v ) + 0.386595;
+			q = x * x + y * ( 0.19600 * y - 0.25472 * x );
+
+			if( q < 0.27597 )
+			{
+				break;
+			}
+
+		} while( q > 0.27846 || v * v > -4.0 * log( u ) * u * u );
+
+		return( v / u );
+	}
+
+	/**
+	 * Function generates a Gaussian (normal)-distributed pseudo-random number
+	 * with the specified mean and std.dev.
+	 */
+
+	double getNorm( const double mean, const double stddev )
+	{
+		return( mean + stddev * getNorm() );
+	}
+
+	/**
+	 * @return The next random bit from the bit pool. Usually used for
+	 * efficient 50% probability evaluations.
+	 */
+
+	int getBit()
+	{
+		if( BitsLeft == 0 )
+		{
+			BitPool = getRaw();
+
+			const int b = (int) ( BitPool & 1 );
+
+			BitsLeft = sizeof( stype ) * 8 - 1;
+			BitPool >>= 1;
+
+			return( b );
+		}
+
+		const int b = (int) ( BitPool & 1 );
+
+		BitsLeft--;
+		BitPool >>= 1;
+
+		return( b );
+	}
+
+	/**
+	 * @return PRNG period's exponent (2^N) estimation.
+	 */
+
+	static size_t getPeriodExp()
+	{
+		return(( fuse * 8 + fuse * 4 + hcount * 8 ) * sizeof( stype ) -
+			hcount - cs );
+	}
+
+protected:
+	stype Seed[ fuse ]; ///< PRNG seeds (>1 - fused).
+	stype lcg[ fuse ]; ///< PRNG lcg (>1 - fused).
+	stype Hash[ hcount ]; ///< PRNG hash array.
+	size_t hpos; ///< Hash array position (increments linearly, resets to 0).
+	stype BitPool; ///< Bit pool, optional feature.
+	int BitsLeft; ///< The number of bits left in the bit pool.
+
+	/**
+	 * @return Inverse multiplier to scale stype's value range to [0; 1)
+	 * range.
+	 */
+
+	static double im()
+	{
+		static const double v = 0.5 / ( 1ULL << ( sizeof( stype ) * 8 - 1 ));
+
+		return( v );
+	}
+};
+
+#endif // GRADILAC_INCLUDED

prvhash.mod/prvhash/gradilac_sat.py

@@ -0,0 +1,183 @@
+# gradilac/prvhash 4.3.1 fuse=1 CSPRNG (XOR) SAT solving simulation -
+# finds a key specified in seed_i, lcg_i, and hcv[].
+# requires autosat from https://github.com/petersn/autosat
+# and python-sat
+#
+# use "time python gradilac_sat.py" to measure solving time.
+# increase "bits" (an even value) and "hci" to estimate solving complexity.
+# "bits=64" corresponds to uint64_t variable size. a minimal reasonable "bits"
+# value is 6; lower values solve instantly. the time exponent dependence on
+# "hci" itself depends on "bits" asymptotically, with higher "bits" values
+# producing a more linear "hci*bits" exponent.
+
+import autosat
+
+##### simulation parameters
+
+bits = 6 # state variable size
+hci = 2 # number of hash elements in use
+
+seed_i = 4 # prng init
+lcg_i = 5 # prng init
+hcv = [13,4,13,3,4,14,12,5,12,15,6,1,9,13,1,15,12,6,11,4,8,5,9,12,13,0,2,1,9,12,15,11] # hash init (hci)
+
+hc = hci # hash array length
+num_obs = 64 # number of observations to use for solving
+
+#####
+
+def inibits(inst,l,ini):
+    result = []
+    for i in range(l):
+        if( (ini>>i)&1 ):
+            v=True
+        else:
+            v=False
+        result.append(inst.get_constant(v))
+    return result
+
[email protected]
+def full_adder(a, b, carry_in):
+    r = a + b + carry_in
+    return r & 1, (r & 2) >> 1
+
+def add(a, b):
+    assert len(a) == len(b)
+    carry = False
+    result = []
+    for a_bit, b_bit in zip(a, b):
+        sum_bit, carry = full_adder(a_bit, b_bit, carry)
+        result.append(sum_bit)
+    return result
+
+def xor(a, b):
+    assert len(a) == len(b)
+    return [i ^ j for i, j in zip(a, b)]
+
+def and_(a, b):
+    assert len(a) == len(b)
+    return [i & j for i, j in zip(a, b)]
+
+def mul(a, b):
+    assert len(a) == len(b)
+    result = [a[0] & bit for bit in b]
+    for i in range(1, len(a)):
+        addend = [a[i] & bit for bit in b[:-i]]
+        result[i:] = add(result[i:], addend)
+    return result
+
+obs = [] # observations
+bits2 = bits>>1
+bmask = (1<<bits)-1
+rawbits5 = 0
+rawbitsA = 0
+
+for i in range(bits2):
+    rawbits5 <<= 2
+    rawbits5 |= 0x1
+    rawbitsA <<= 2
+    rawbitsA |= 0x2
+
+def prvhash_core_calc(seed, lcg, h):
+    seed = seed * ( lcg * 2 + 1 )
+    seed &= bmask
+    rs = seed>>bits2 | seed<<bits2
+    rs &= bmask
+    h += rs + rawbitsA
+    h &= bmask
+    lcg += seed + rawbits5
+    lcg &= bmask
+    seed ^= h
+    out = lcg ^ rs
+    return seed, lcg, h, out
+
+# calculate real outputs
+
+calc_seed = seed_i&bmask
+calc_lcg = lcg_i&bmask
+calc_h = []
+
+for i in range(hc):
+    if(i < hci):
+        calc_h.append(hcv[i]&bmask)
+    else:
+        calc_h.append(0)
+
+calc_x = 0
+
+for i in range(5):
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+
+for i in range(hc+1):
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+    calc_x += 1
+
+for i in range(num_obs):
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+    calc_x += 1
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out2 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+    calc_x += 1
+
+    obs.append(out1^out2)
+
+print("----")
+
+# solve initial state
+
+inst = autosat.Instance()
+
+BITR5 = inibits(inst, bits, rawbits5)
+BITRA = inibits(inst, bits, rawbitsA)
+
+def prvhash_core_sat(seed, lcg, h):
+    seed = mul(seed, [True] + lcg[:-1])
+    rs = seed[bits2:] + seed[:bits2]
+    h = add(h, add(rs, BITRA))
+    lcg = add(lcg, add(seed, BITR5))
+    seed = xor(seed, h)
+    out = xor(lcg, rs)
+    return seed, lcg, h, out
+
+start_seed = inst.new_vars(bits)
+start_lcg = inst.new_vars(bits)
+start_h = []
+
+seed = start_seed[:]
+lcg = start_lcg[:]
+h = []
+
+for i in range(hc):
+    if(i < hci):
+        start_h.append(inst.new_vars(bits))
+        h.append(start_h[i][:])
+    else:
+        h.append(inibits(inst, bits, 0))
+
+x = 0
+
+for k in range(5):
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+
+for k in range(hc+1):
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+    x += 1
+
+for k in range(num_obs):
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+    x += 1
+    seed, lcg, h[x % hc], out2 = prvhash_core_sat(seed, lcg, h[x % hc])
+    x += 1
+
+    out = xor(out1, out2)
+
+    for i, b in enumerate(out):
+        b.make_equal(bool((obs[k] >> i) & 1))
+
+model = inst.solve(solver_name="Glucose3",decode_model=False)
+#print(model)
+
+print("seed = %4i (%4i)" % (autosat.decode_number(start_seed, model), (seed_i&bmask)))
+print("lcg  = %4i (%4i)" % (autosat.decode_number(start_lcg, model), (lcg_i&bmask)))
+
+for i in range(hci):
+    print("hash = %4i (%4i)" % (autosat.decode_number(start_h[i], model), (hcv[i]&bmask)))

prvhash.mod/prvhash/proof_christmas_tree.c

@@ -0,0 +1,72 @@
+/**
+ * proof_christmas_tree.c (prvhash1) version 4.3.3
+ *
+ * Program reads certain "prvhash1" data and represents it as two-dimensional
+ * ASCII-art. Generates HTML to stdout.
+ * 
+ * License
+ *
+ * Copyright (c) 2022 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#include <stdio.h>
+#include <stdint.h>
+#define PH_HASH_COUNT 200
+#define READ_MODE 1 // 0 or 1
+#define READ_WIDTH ( PH_HASH_COUNT + 1 )
+#define READ_HEIGHT ( READ_WIDTH * 32 )
+static inline uint8_t prvhash_core1( uint8_t* const Seed,
+	uint8_t* const lcg, uint8_t* const Hash )
+{
+	*Hash ^= (uint8_t) ( *Seed ^ 0x1 );
+	*lcg ^= (uint8_t) ( *Seed ^ READ_MODE );
+	const uint8_t out = (uint8_t) ( *lcg ^ *Seed );
+	*Seed ^= *Hash;
+	return( out & 1 );
+}
+int main()
+{
+	uint8_t Seed = 0, lcg = 0;
+	uint8_t Hash[ PH_HASH_COUNT ] = { 0 };
+	int HashPos = 0;
+	printf( "<html><head>"
+		"<style>body{font: 1px Courier; line-height: 1px;}</style>\n" );
+	printf( "</head><body><pre>\n" );
+
+	for( int i = 0; i < PH_HASH_COUNT + 2; i++ ) // Remove pixel offset.
+	{
+		prvhash_core1( &Seed, &lcg, Hash + HashPos );
+		if( ++HashPos == PH_HASH_COUNT ) HashPos = 0;
+	}
+	for( int l = 0; l < READ_HEIGHT; l++ )
+	{
+		for( int k = 0; k < READ_WIDTH; k++ )
+		{
+			if( prvhash_core1( &Seed, &lcg, Hash + HashPos ))
+				printf( "0" );
+			else
+				printf( " " );
+			if( ++HashPos == PH_HASH_COUNT ) HashPos = 0;
+		}
+		printf( "\n" );
+	}
+	printf( "</pre></body>\n</html>\n" );
+}

prvhash.mod/prvhash/proof_fine_art.c

@@ -0,0 +1,81 @@
+/**
+ * proof_fine_art.c (prvhash1) version 4.3.4
+ *
+ * Program reads "prvhash1" data and builds a colored image using multi-pass
+ * approach. Produces a JPG image using "stb_image_write" library.
+ * 
+ * License
+ *
+ * Copyright (c) 2022 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#include <stdint.h>
+// !!! Requires "stb_image_write.h" from https://github.com/nothings/stb
+#define STB_IMAGE_WRITE_IMPLEMENTATION
+#include "stb_image_write.h"
+
+#define PH_HASH_COUNT 1638 // 1365, 1366, 1638, or 2046
+#define PH_READ_MODE 1 // 0 or 1
+#define PH_SEED_COUNT 1 // 1-4, powers of 2
+#define WIDTH ( PH_HASH_COUNT + 1 )
+#define HEIGHT 2048
+#define CHN 3
+#define PASS_COUNT 127
+#define MSH 1
+static inline uint8_t prvhash_core1( uint8_t* const Seed,
+	uint8_t* const lcg, uint8_t* const Hash )
+{
+	*Hash ^= (uint8_t) ( *Seed ^ 1 );
+	*lcg ^= (uint8_t) ( *Seed ^ PH_READ_MODE );
+	const uint8_t out = (uint8_t) ( *lcg ^ *Seed );
+	*Seed ^= *Hash;
+	return( out );
+}
+int main()
+{
+	uint8_t Seed[ PH_SEED_COUNT ] = { 0 }, lcg = 0;
+	uint8_t Hash[ PH_HASH_COUNT ] = { 0 };
+	uint8_t Seed2[ PH_SEED_COUNT ] = { 0 }, lcg2 = 0;
+	uint8_t Hash2[ PH_HASH_COUNT ] = { 0 };
+	uint8_t Seed3[ PH_SEED_COUNT ] = { 0 }, lcg3 = 0;
+	uint8_t Hash3[ PH_HASH_COUNT ] = { 0 };
+	int i, HashPos = 0, SeedPos = 0;
+	for( i = 0; i < PH_HASH_COUNT; i += 2 ) { Hash2[ i ] = 1; }
+	for( i = 0; i < PH_HASH_COUNT; i += 3 ) { Hash3[ i ] = 1; }
+
+	uint8_t* img = (uint8_t*) malloc( WIDTH * HEIGHT * CHN );
+	memset( img, 0, WIDTH * HEIGHT * CHN );
+	for( i = 0; i < PASS_COUNT; i++ )
+	{
+		uint8_t* op = img;
+		for( int l = 0; l < WIDTH * HEIGHT; l++ )
+		{
+			op[ 0 ] += prvhash_core1( Seed + SeedPos, &lcg, Hash + HashPos ) << MSH;
+			op[ 2 ] += prvhash_core1( Seed2 + SeedPos, &lcg2, Hash2 + HashPos ) << MSH;
+			op[ 1 ] += prvhash_core1( Seed3 + SeedPos, &lcg3, Hash3 + HashPos ) << MSH;
+			if( ++HashPos == PH_HASH_COUNT ) HashPos = 0;
+			if( ++SeedPos == PH_SEED_COUNT ) SeedPos = 0;
+			op += CHN;
+		}
+	}
+	stbi_write_jpg( "prvhash1-2048.jpg", WIDTH, HEIGHT, CHN, img, 90 );
+	free( img );
+}

prvhash.mod/prvhash/proof_math_is_engineered.c

@@ -0,0 +1,66 @@
+/**
+ * proof_math_is_engineered.c (prvhash1) version 4.3.2
+ *
+ * "Someone" was already smart even before the "Big Bang". Math is an
+ * engineered construct, with a built-in ROM.
+ *
+ * License
+ *
+ * Copyright (c) 2022 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#include <stdio.h>
+#include <stdint.h>
+#define PH_HASH_COUNT 15
+#define READ_MODE 0 // 0 or 1
+#define READ_WORD_BITS 16
+#define READ_COUNT 512
+#define READ_BIT_ORDER 0 // 0 or 1
+static inline uint8_t prvhash_core1( uint8_t* const Seed,
+	uint8_t* const lcg, uint8_t* const Hash )
+{
+	*Hash ^= (uint8_t) ( *Seed ^ 0x1 );
+	*lcg ^= (uint8_t) ( *Seed ^ READ_MODE );
+	const uint8_t out = (uint8_t) ( *lcg ^ *Seed );
+	*Seed ^= *Hash;
+	return( out & 1 );
+}
+int main()
+{
+	uint8_t Seed = 0, lcg = 0;
+	uint8_t Hash[ PH_HASH_COUNT ] = { 0 };
+	int HashPos = 0;
+	for( int l = 0; l < READ_COUNT; l++ )
+	{
+		uint64_t r = 0;
+		for( int k = 0; k < READ_WORD_BITS; k++ )
+		{
+			#if READ_BIT_ORDER == 0
+			r <<= 1;
+			r |= prvhash_core1( &Seed, &lcg, Hash + HashPos );
+			#else // READ_BIT_ORDER == 0
+			r |= (uint64_t) prvhash_core1( &Seed, &lcg, Hash + HashPos ) << k;
+			#endif // READ_BIT_ORDER == 0
+			if( ++HashPos == PH_HASH_COUNT ) HashPos = 0;
+		}
+		printf( "%llu\n", r );
+	}
+}

prvhash.mod/prvhash/proof_reptile.c

@@ -0,0 +1,73 @@
+/**
+ * proof_reptile.c (prvhash1) version 4.3.1
+ *
+ * Program reads "prvhash1" data and builds a black-and-white image using
+ * multi-pass approach. Produces a JPG image using "stb_image_write" library.
+ * 
+ * License
+ *
+ * Copyright (c) 2022-2023 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#include <stdint.h>
+// !!! Requires "stb_image_write.h" from https://github.com/nothings/stb
+#define STB_IMAGE_WRITE_IMPLEMENTATION
+#include "stb_image_write.h"
+
+#define PH_HASH_COUNT 2046 // 1365, 1366, 1638, or 2046
+#define PH_SEED_COUNT 32 // 1-4, powers of 2
+#define WIDTH ( PH_HASH_COUNT + 1 )
+#define HEIGHT 2048
+#define CHN 3
+#define PASS_COUNT 127
+#define MSH 1
+static inline uint8_t prvhash_core1_min( uint8_t* const Seed,
+	uint8_t* const Hash )
+{
+	*Hash ^= (uint8_t) ( *Seed ^ 1 );
+	const uint8_t out = *Seed;
+	*Seed ^= *Hash;
+	return( out );
+}
+int main()
+{
+	uint8_t Seed[ PH_SEED_COUNT ] = { 0 };
+	uint8_t Hash[ PH_HASH_COUNT ] = { 0 };
+	int i, HashPos = 0, SeedPos = 0;
+
+	uint8_t* img = (uint8_t*) malloc( WIDTH * HEIGHT * CHN );
+	memset( img, 0, WIDTH * HEIGHT * CHN );
+	for( i = 0; i < PASS_COUNT; i++ )
+	{
+		uint8_t* op = img;
+		for( int l = 0; l < WIDTH * HEIGHT; l++ )
+		{
+			op[ 0 ] += prvhash_core1_min( Seed + SeedPos, Hash + HashPos ) << MSH;
+			op[ 1 ] = op[ 0 ];
+			op[ 2 ] = op[ 1 ];
+			if( ++HashPos == PH_HASH_COUNT ) HashPos = 0;
+			if( ++SeedPos == PH_SEED_COUNT ) SeedPos = 0;
+			op += CHN;
+		}
+	}
+	stbi_write_jpg( "prvhash1-2048.jpg", WIDTH, HEIGHT, CHN, img, 95 );
+	free( img );
+}

prvhash.mod/prvhash/prvhash16.h

@@ -0,0 +1,161 @@
+/**
+ * prvhash16.h version 4.3.1
+ *
+ * The inclusion file for the "prvhash16" hash function. For demonstration
+ * purposes, not practically useful.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ *
+ * License
+ *
+ * Copyright (c) 2020-2023 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#ifndef PRVHASH16_INCLUDED
+#define PRVHASH16_INCLUDED
+
+#include "prvhash_core.h"
+
+/**
+ * PRVHASH hash function (16-bit variables). Produces a hash of the specified
+ * message, string, or binary data block. This function does not apply
+ * endianness correction to the resulting hash.
+ *
+ * @param Msg0 The message to produce a hash from. The alignment of this
+ * pointer is unimportant.
+ * @param MsgLen Message's length, in bytes.
+ * @param[out] Hash0 The resulting hash. The length of this buffer should be
+ * equal to HashLen. On systems where this is relevant, this address should be
+ * aligned to 32 bits.
+ * @param HashLen The required hash length, in bytes; should be >= 4, in
+ * increments of 2; no higher-value limits.
+ * @param UseSeed Optional value, to use instead of the default seed. To use
+ * the default seed, set to 0. The UseSeed value can have any bit length and
+ * any statistical quality, and is used only as an additional entropy source.
+ */
+
+static inline void prvhash16( const void* const Msg0, const size_t MsgLen,
+	void* const Hash0, const size_t HashLen, uint32_t UseSeed )
+{
+	const uint8_t* Msg = (const uint8_t*) Msg0;
+	uint8_t* const Hash = (uint8_t*) Hash0;
+
+	memset( Hash, 0, HashLen );
+
+	typedef uint16_t state_t;
+
+	state_t Seed = 0x128D; // The state after 5 PRVHASH rounds from the
+	state_t lcg = 0x8D5B; // "zero-state".
+	*(state_t*) Hash = 0x0932;
+
+	const state_t* const HashEnd = (state_t*) ( Hash + HashLen );
+	state_t* hc = (state_t*) Hash;
+	state_t fbm = 0x0101;
+
+	if( MsgLen > 0 )
+	{
+		fbm <<= ( Msg[ MsgLen - 1 ] >> 7 );
+	}
+
+	size_t k;
+
+	if( UseSeed != 0 )
+	{
+		for( k = 0; k < 2; k++ )
+		{
+			Seed ^= (state_t) UseSeed;
+			lcg ^= (state_t) UseSeed;
+
+			prvhash_core16( &Seed, &lcg, hc );
+
+			if( ++hc == HashEnd )
+			{
+				hc = (state_t*) Hash;
+			}
+
+			UseSeed >>= 16;
+		}
+	}
+
+	const uint8_t* const MsgEnd = Msg + MsgLen;
+
+	while( Msg <= MsgEnd )
+	{
+		state_t msgw;
+
+		if( Msg < MsgEnd )
+		{
+			msgw = *Msg;
+		}
+		else
+		{
+			msgw = (state_t) ( fbm & 0xFF );
+			fbm = 0;
+		}
+
+		if( Msg < MsgEnd - 1 )
+		{
+			msgw |= (state_t) ( (state_t) Msg[ 1 ] << 8 );
+		}
+		else
+		{
+			msgw |= (state_t) ( fbm & 0xFF00 );
+			fbm = 0;
+		}
+
+		Seed ^= msgw;
+		lcg ^= msgw;
+
+		prvhash_core16( &Seed, &lcg, hc );
+
+		if( ++hc == HashEnd )
+		{
+			hc = (state_t*) Hash;
+		}
+
+		Msg += sizeof( state_t );
+	}
+
+	const size_t fc = HashLen + ( MsgLen < HashLen - sizeof( state_t ) ?
+		(uint8_t*) HashEnd - (uint8_t*) hc : 0 );
+
+	for( k = 0; k <= fc; k += sizeof( state_t ))
+	{
+		prvhash_core16( &Seed, &lcg, hc );
+
+		if( ++hc == HashEnd )
+		{
+			hc = (state_t*) Hash;
+		}
+	}
+
+	for( k = 0; k < HashLen; k += sizeof( state_t ))
+	{
+		*hc = prvhash_core16( &Seed, &lcg, hc );
+
+		if( ++hc == HashEnd )
+		{
+			hc = (state_t*) Hash;
+		}
+	}
+}
+
+#endif // PRVHASH16_INCLUDED

prvhash.mod/prvhash/prvhash64.h

@@ -0,0 +1,253 @@
+/**
+ * prvhash64.h version 4.3.3
+ *
+ * The inclusion file for the "prvhash64" and "prvhash64_64m" hash functions.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ *
+ * License
+ *
+ * Copyright (c) 2020-2023 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#ifndef PRVHASH64_INCLUDED
+#define PRVHASH64_INCLUDED
+
+#include "prvhash_core.h"
+
+#define PRH64_T uint64_t // PRVHASH state variable type.
+#define PRH64_S sizeof( PRH64_T ) // State variable type's size.
+#define PRH64_Sm1 ( PRH64_S - 1 ) // = PRH64_S - 1.
+#define PRH64_FN prvhash_core64 // PRVHASH function name.
+#define PRH64_LUEC( v ) prvhash_lu64ec( v ) // Value load function, with EC.
+#define PRH64_LPUEC prvhash_lpu64ec // Value load function, pad, EC.
+#define PRH64_EC( v ) PRVHASH_EC64( v ) // Value endianness-correction.
+
+/**
+ * Function loads 64-bit message word and pads it with the "final byte". This
+ * function should only be called if there are less than 8 bytes left to read.
+ * Function performs endianness-correction automatically.
+ *
+ * @param Msg Message pointer, alignment is unimportant. Should be below or
+ * equal to MsgEnd.
+ * @param MsgEnd Message's end pointer.
+ * @param fb Final byte used for padding.
+ */
+
+static PRVHASH_INLINE uint64_t prvhash_lpu64ec( const uint8_t* const Msg,
+	const uint8_t* const MsgEnd, uint64_t fb )
+{
+	const size_t MsgLen = MsgEnd - Msg;
+	const int ml8 = (int) ( MsgLen * 8 );
+
+	if( MsgLen < 4 )
+	{
+		if( MsgLen != 0 )
+		{
+			fb = fb << ml8 | Msg[ 0 ];
+
+			if( MsgLen > 1 )
+			{
+				fb |= (uint64_t) Msg[ 1 ] << 8;
+
+				if( MsgLen > 2 )
+				{
+					fb |= (uint64_t) Msg[ 2 ] << 16;
+				}
+			}
+		}
+
+		return( fb );
+	}
+
+	const uint64_t mh = prvhash_lu32ec( MsgEnd - 4 );
+	const uint64_t ml = prvhash_lu32ec( Msg );
+
+	return( fb << ml8 | ml | ( mh >> ( 64 - ml8 )) << 32 );
+}
+
+/**
+ * PRVHASH hash function (64-bit variables). Produces a hash of the specified
+ * message, string, or binary data block. This function applies
+ * endianness-correction to the resulting hash automatically (on little- and
+ * big-endian processors).
+ *
+ * @param Msg0 The message to produce a hash from. The alignment of this
+ * pointer is unimportant.
+ * @param MsgLen Message's length, in bytes.
+ * @param[out] HashOut The resulting hash. The length of this buffer should
+ * be equal to HashLen. On systems where this is relevant, this address should
+ * be aligned to PRH64_S bytes.
+ * @param HashLen The required hash length, in bytes; should be >= PRH64_S,
+ * in increments of PRH64_S; no higher-value limits.
+ * @param UseSeed Optional value, to use instead of the default seed. To use
+ * the default seed, set to 0. The UseSeed value can have any bit length and
+ * statistical quality, and is used only as an additional entropy source. If
+ * this value is shared between big- and little-endian systems, it should be
+ * endianness-corrected.
+ */
+
+static inline void prvhash64( const void* const Msg0, const size_t MsgLen,
+	void* const HashOut, const size_t HashLen, const PRH64_T UseSeed )
+{
+	const uint8_t* Msg = (const uint8_t*) Msg0;
+	uint8_t* const Hash = (uint8_t*) HashOut;
+
+	memset( Hash, 0, HashLen );
+
+	PRH64_T Seed = 0x217992B44669F46A; // The state after 5 PRVHASH rounds
+	PRH64_T lcg = 0xB5E2CC2FE9F0B35B; // from the "zero-state".
+	*(PRH64_T*) Hash = 0x949B5E0A608D76D5 ^ UseSeed;
+
+	const uint8_t* const MsgEnd = Msg + MsgLen;
+	const PRH64_T* const HashEnd = (PRH64_T*) ( Hash + HashLen );
+	PRH64_T* hc = (PRH64_T*) Hash;
+
+	PRH64_T fb = 1;
+
+	if( MsgLen != 0 )
+	{
+		fb <<= ( MsgEnd[ -1 ] >> 7 );
+	}
+
+	while( 1 )
+	{
+		PRH64_T msgw;
+
+		if( Msg < MsgEnd - PRH64_Sm1 )
+		{
+			msgw = PRH64_LUEC( Msg );
+		}
+		else
+		{
+			if( Msg > MsgEnd )
+			{
+				break;
+			}
+
+			msgw = PRH64_LPUEC( Msg, MsgEnd, fb );
+		}
+
+		Seed ^= msgw;
+		lcg ^= msgw;
+
+		PRH64_FN( &Seed, &lcg, hc );
+
+		if( ++hc == HashEnd )
+		{
+			hc = (PRH64_T*) Hash;
+		}
+
+		Msg += PRH64_S;
+	}
+
+	const size_t fc = ( HashLen == PRH64_S ? 0 :
+		HashLen + ( MsgLen < HashLen - PRH64_S ?
+		(uint8_t*) HashEnd - (uint8_t*) hc : 0 ));
+
+	size_t k;
+
+	for( k = 0; k <= fc; k += PRH64_S )
+	{
+		PRH64_FN( &Seed, &lcg, hc );
+
+		if( ++hc == HashEnd )
+		{
+			hc = (PRH64_T*) Hash;
+		}
+	}
+
+	for( k = 0; k < HashLen; k += PRH64_S )
+	{
+		*hc = PRH64_EC( PRH64_FN( &Seed, &lcg, hc ));
+
+		if( ++hc == HashEnd )
+		{
+			hc = (PRH64_T*) Hash;
+		}
+	}
+}
+
+/**
+ * PRVHASH hash function. Produces and returns a 64-bit hash of the specified
+ * message, string, or binary data block. This is a "minimal" implementation,
+ * designed for 64-bit hash-table and hash-map uses. Equivalent to the
+ * "prvhash64" function with HashLen == 8, but returns an immediate result
+ * (endianness-correction is not required).
+ *
+ * @param Msg0 The message to produce a hash from. The alignment of this
+ * pointer is unimportant.
+ * @param MsgLen Message's length, in bytes.
+ * @param UseSeed Optional value, to use instead of the default seed. To use
+ * the default seed, set to 0. The UseSeed value can have any bit length and
+ * statistical quality, and is used only as an additional entropy source. If
+ * this value is shared between big- and little-endian systems, it should be
+ * endianness-corrected.
+ */
+
+static inline uint64_t prvhash64_64m( const void* const Msg0,
+	const size_t MsgLen, const PRH64_T UseSeed )
+{
+	const uint8_t* Msg = (const uint8_t*) Msg0;
+
+	PRH64_T Seed = 0x217992B44669F46A; // The state after 5 PRVHASH rounds
+	PRH64_T lcg = 0xB5E2CC2FE9F0B35B; // from the "zero-state".
+	PRH64_T Hash = 0x949B5E0A608D76D5 ^ UseSeed;
+
+	const uint8_t* const MsgEnd = Msg + MsgLen;
+
+	PRH64_T fb = 1;
+
+	if( MsgLen != 0 )
+	{
+		fb <<= ( MsgEnd[ -1 ] >> 7 );
+	}
+
+	while( 1 )
+	{
+		PRH64_T msgw;
+
+		if( Msg < MsgEnd - PRH64_Sm1 )
+		{
+			msgw = PRH64_LUEC( Msg );
+		}
+		else
+		{
+			if( Msg > MsgEnd )
+			{
+				PRH64_FN( &Seed, &lcg, &Hash );
+
+				return( PRH64_FN( &Seed, &lcg, &Hash ));
+			}
+
+			msgw = PRH64_LPUEC( Msg, MsgEnd, fb );
+		}
+
+		Seed ^= msgw;
+		lcg ^= msgw;
+
+		PRH64_FN( &Seed, &lcg, &Hash );
+
+		Msg += PRH64_S;
+	}
+}
+
+#endif // PRVHASH64_INCLUDED

prvhash.mod/prvhash/prvhash64s.h

@@ -0,0 +1,387 @@
+/**
+ * prvhash64s.h version 4.3.3
+ *
+ * The inclusion file for the "prvhash64s" hash function. More secure,
+ * streamed, and high-speed. Implements a fused variant of the "prvhash64"
+ * hash function, with output PRNG XORing, and a self-start.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ *
+ * License
+ *
+ * Copyright (c) 2020-2023 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#ifndef PRVHASH64S_INCLUDED
+#define PRVHASH64S_INCLUDED
+
+#include "prvhash_core.h"
+
+#define PRH64S_T uint64_t // PRVHASH state variable type.
+#define PRH64S_S sizeof( PRH64S_T ) // State variable type's size.
+#define PRH64S_FN prvhash_core64 // PRVHASH function name.
+#define PRH64S_LUEC( v ) prvhash_lu64ec( v ) // Value load function, with EC.
+#define PRH64S_EC( v ) PRVHASH_EC64( v ) // Value's endianness-correction.
+
+#define PRH64S_MAX 512 // Maximal supported hash length, in bytes.
+#define PRH64S_FUSE 4 // PRVHASH fusing.
+#define PRH64S_LEN ( PRH64S_S * PRH64S_FUSE ) // Intermediate block's length.
+
+/**
+ * The context structure of the "prvhash64s_X" functions. On systems where
+ * this is relevant, this structure should be aligned to PRH64S_S bytes.
+ * This structure, being small, can be placed on stack.
+ */
+
+typedef struct {
+	PRH64S_T Seed[ PRH64S_FUSE ]; ///< Current fused "Seed" values.
+	PRH64S_T lcg[ PRH64S_FUSE ]; ///< Current fused "lcg" values.
+	uint8_t Hash[ PRH64S_MAX ]; ///< Working hash buffer.
+	uint8_t Block[ PRH64S_LEN ]; ///< Intermediate input data block.
+	uint64_t MsgLen; ///< Message length counter, in bytes.
+	size_t HashLen; ///< Hash buffer length, in bytes, >= PRH64S_S,
+		///< increments of PRH64S_S.
+	size_t HashPos; ///< Hash buffer position.
+	size_t BlockFill; ///< The number of bytes filled in the Block.
+	uint8_t fb; ///< Final stream byte value, for hashing finalization.
+} PRVHASH64S_CTX;
+
+/**
+ * PRVHASH64S streaming hash function initialization (64-bit state variables)
+ * This function should be called before the hashing session.
+ *
+ * @param[out] ctx Context structure. Should be aligned to PRH64S_S bytes.
+ * @param HashLen The required hash length, in bytes; should be >= PRH64S_S,
+ * in increments of PRH64S_S. Should not exceed PRH64S_MAX.
+ * @param UseSeeds Optional pointer to seed entropy pool, to use instead of
+ * the default seeds. To use the default seeds, set to 0. If specified, the
+ * UseSeeds should point to a 32-byte array (e.g., four 64-bit values), which
+ * can have any statistical quality, and can be partially set to zero. The
+ * address alignment of this pointer is unimportant. The provided values will
+ * be endianness-corrected automatically.
+ */
+
+static inline void prvhash64s_init( PRVHASH64S_CTX* const ctx,
+	const size_t HashLen, const void* const UseSeeds )
+{
+	memset( ctx -> Hash, 0, HashLen );
+	int i;
+
+	if( UseSeeds == 0 )
+	{
+		for( i = 0; i < PRH64S_FUSE; i++ )
+		{
+			ctx -> Seed[ i ] = 0;
+			ctx -> lcg[ i ] = 0;
+		}
+	}
+	else
+	{
+		for( i = 0; i < PRH64S_FUSE; i++ )
+		{
+			ctx -> Seed[ i ] = PRH64S_LUEC( (const uint8_t*) UseSeeds +
+				i * PRH64S_S );
+
+			ctx -> lcg[ i ] = 0;
+		}
+	}
+
+	ctx -> MsgLen = 0;
+	ctx -> HashLen = HashLen;
+	ctx -> HashPos = 0;
+	ctx -> BlockFill = 0;
+	ctx -> fb = 0;
+
+	PRH64S_T* const hc = (PRH64S_T*) ctx -> Hash;
+
+	PRH64S_T Seed1 = ctx -> Seed[ 0 ];
+	PRH64S_T Seed2 = ctx -> Seed[ 1 ];
+	PRH64S_T Seed3 = ctx -> Seed[ 2 ];
+	PRH64S_T Seed4 = ctx -> Seed[ 3 ];
+	PRH64S_T lcg1 = ctx -> lcg[ 0 ];
+	PRH64S_T lcg2 = ctx -> lcg[ 1 ];
+	PRH64S_T lcg3 = ctx -> lcg[ 2 ];
+	PRH64S_T lcg4 = ctx -> lcg[ 3 ];
+
+	for( i = 0; i < PRVHASH_INIT_COUNT; i++ )
+	{
+		PRH64S_FN( &Seed1, &lcg1, hc );
+		PRH64S_FN( &Seed2, &lcg2, hc );
+		PRH64S_FN( &Seed3, &lcg3, hc );
+		PRH64S_FN( &Seed4, &lcg4, hc );
+	}
+
+	ctx -> Seed[ 0 ] = Seed1;
+	ctx -> Seed[ 1 ] = Seed2;
+	ctx -> Seed[ 2 ] = Seed3;
+	ctx -> Seed[ 3 ] = Seed4;
+	ctx -> lcg[ 0 ] = lcg1;
+	ctx -> lcg[ 1 ] = lcg2;
+	ctx -> lcg[ 2 ] = lcg3;
+	ctx -> lcg[ 3 ] = lcg4;
+}
+
+/**
+ * This function updates the hash according to the contents of the message.
+ * Before this function can be called, the prvhash64s_init() should be called,
+ * to initialize the context structure. When the streamed hashing is finished,
+ * the prvhash64s_final() function should be called.
+ *
+ * @param[in,out] ctx Context structure.
+ * @param Msg0 The message to produce a hash from. The address alignment of
+ * this pointer is unimportant. Can be 0 if MsgLen==0.
+ * @param MsgLen Message's length, in bytes; can be 0.
+ */
+
+static inline void prvhash64s_update( PRVHASH64S_CTX* const ctx,
+	const void* const Msg0, size_t MsgLen )
+{
+	if( MsgLen == 0 )
+	{
+		return;
+	}
+
+	ctx -> MsgLen += (uint64_t) MsgLen;
+
+	const uint8_t* Msg = (const uint8_t*) Msg0;
+	size_t blf = ctx -> BlockFill;
+
+	if( blf + MsgLen >= PRH64S_LEN && blf != 0 )
+	{
+		const size_t CopyLen = PRH64S_LEN - blf;
+		memcpy( ctx -> Block + blf, Msg, CopyLen );
+		blf = 0;
+
+		Msg += CopyLen;
+		MsgLen -= CopyLen;
+
+		PRH64S_T* const hc = (PRH64S_T*) ( ctx -> Hash + ctx -> HashPos );
+
+		ctx -> HashPos += PRH64S_S;
+
+		if( ctx -> HashPos == ctx -> HashLen )
+		{
+			ctx -> HashPos = 0;
+		}
+
+		const PRH64S_T m1 = PRH64S_LUEC( ctx -> Block );
+		const PRH64S_T m2 = PRH64S_LUEC( ctx -> Block + PRH64S_S );
+		const PRH64S_T m3 = PRH64S_LUEC( ctx -> Block + PRH64S_S * 2 );
+		const PRH64S_T m4 = PRH64S_LUEC( ctx -> Block + PRH64S_S * 3 );
+
+		ctx -> Seed[ 0 ] ^= m1;
+		ctx -> lcg[ 0 ] ^= m1;
+		PRH64S_FN( &ctx -> Seed[ 0 ], &ctx -> lcg[ 0 ], hc );
+
+		ctx -> Seed[ 1 ] ^= m2;
+		ctx -> lcg[ 1 ] ^= m2;
+		PRH64S_FN( &ctx -> Seed[ 1 ], &ctx -> lcg[ 1 ], hc );
+
+		ctx -> Seed[ 2 ] ^= m3;
+		ctx -> lcg[ 2 ] ^= m3;
+		PRH64S_FN( &ctx -> Seed[ 2 ], &ctx -> lcg[ 2 ], hc );
+
+		ctx -> Seed[ 3 ] ^= m4;
+		ctx -> lcg[ 3 ] ^= m4;
+		PRH64S_FN( &ctx -> Seed[ 3 ], &ctx -> lcg[ 3 ], hc );
+	}
+
+	if( MsgLen >= PRH64S_LEN )
+	{
+		const PRH64S_T* const HashEnd =
+			(PRH64S_T*) ( ctx -> Hash + ctx -> HashLen );
+
+		PRH64S_T* hc = (PRH64S_T*) ( ctx -> Hash + ctx -> HashPos );
+
+		PRH64S_T Seed1 = ctx -> Seed[ 0 ];
+		PRH64S_T Seed2 = ctx -> Seed[ 1 ];
+		PRH64S_T Seed3 = ctx -> Seed[ 2 ];
+		PRH64S_T Seed4 = ctx -> Seed[ 3 ];
+		PRH64S_T lcg1 = ctx -> lcg[ 0 ];
+		PRH64S_T lcg2 = ctx -> lcg[ 1 ];
+		PRH64S_T lcg3 = ctx -> lcg[ 2 ];
+		PRH64S_T lcg4 = ctx -> lcg[ 3 ];
+
+		do
+		{
+			const PRH64S_T m1 = PRH64S_LUEC( Msg );
+			const PRH64S_T m2 = PRH64S_LUEC( Msg + PRH64S_S );
+			const PRH64S_T m3 = PRH64S_LUEC( Msg + PRH64S_S * 2 );
+			const PRH64S_T m4 = PRH64S_LUEC( Msg + PRH64S_S * 3 );
+
+			Seed1 ^= m1;
+			lcg1 ^= m1;
+			Seed2 ^= m2;
+			lcg2 ^= m2;
+			Seed3 ^= m3;
+			lcg3 ^= m3;
+			Seed4 ^= m4;
+			lcg4 ^= m4;
+
+			PRH64S_FN( &Seed1, &lcg1, hc );
+			PRH64S_FN( &Seed2, &lcg2, hc );
+			PRH64S_FN( &Seed3, &lcg3, hc );
+			PRH64S_FN( &Seed4, &lcg4, hc );
+
+			Msg += PRH64S_LEN;
+			MsgLen -= PRH64S_LEN;
+
+			if( ++hc == HashEnd )
+			{
+				hc = (PRH64S_T*) ctx -> Hash;
+			}
+
+		} while( MsgLen >= PRH64S_LEN );
+
+		ctx -> Seed[ 0 ] = Seed1;
+		ctx -> Seed[ 1 ] = Seed2;
+		ctx -> Seed[ 2 ] = Seed3;
+		ctx -> Seed[ 3 ] = Seed4;
+		ctx -> lcg[ 0 ] = lcg1;
+		ctx -> lcg[ 1 ] = lcg2;
+		ctx -> lcg[ 2 ] = lcg3;
+		ctx -> lcg[ 3 ] = lcg4;
+		ctx -> HashPos = (uint8_t*) hc - ctx -> Hash;
+	}
+
+	memcpy( ctx -> Block + blf, Msg, MsgLen );
+	ctx -> BlockFill = blf + MsgLen;
+	ctx -> fb = Msg[ MsgLen - 1 ];
+}
+
+/**
+ * This function finalizes the streamed hashing. This function should be
+ * called only after a prior prvhash64s_init() function call; intermediate
+ * prvhash64s_update() function call is not required. This function applies
+ * endianness-correction to the resulting hash value automatically
+ * (on little- and big-endian processors).
+ *
+ * @param[in,out] ctx Context structure. Zeroed on function's return.
+ * @param[out] HashOut The hash buffer to receive the resulting hash value.
+ * Buffer's size should match the HashLen specified during initialization. The
+ * address alignment of this buffer is unimportant.
+ */
+
+static inline void prvhash64s_final( PRVHASH64S_CTX* const ctx,
+	void* const HashOut )
+{
+	uint8_t fbytes[ PRH64S_LEN ];
+	memset( fbytes, 0, PRH64S_LEN );
+
+	fbytes[ PRH64S_S - 1 ] = (uint8_t) ( 1 << ( ctx -> fb >> 7 ));
+	prvhash64s_update( ctx, fbytes, PRH64S_S );
+
+	const uint64_t MsgLen = PRH64S_EC( ctx -> MsgLen );
+	prvhash64s_update( ctx, &MsgLen, 8 );
+	fbytes[ PRH64S_S - 1 ] = (uint8_t) ( 1 << ( ctx -> fb >> 7 ));
+	prvhash64s_update( ctx, fbytes, PRH64S_S );
+
+	if( ctx -> BlockFill > 0 )
+	{
+		fbytes[ PRH64S_S - 1 ] = 0;
+		prvhash64s_update( ctx, fbytes, PRH64S_LEN - ctx -> BlockFill );
+	}
+
+	const PRH64S_T* const HashEnd =
+		(PRH64S_T*) ( ctx -> Hash + ctx -> HashLen );
+
+	PRH64S_T* hc = (PRH64S_T*) ( ctx -> Hash + ctx -> HashPos );
+
+	PRH64S_T Seed1 = ctx -> Seed[ 0 ];
+	PRH64S_T Seed2 = ctx -> Seed[ 1 ];
+	PRH64S_T Seed3 = ctx -> Seed[ 2 ];
+	PRH64S_T Seed4 = ctx -> Seed[ 3 ];
+	PRH64S_T lcg1 = ctx -> lcg[ 0 ];
+	PRH64S_T lcg2 = ctx -> lcg[ 1 ];
+	PRH64S_T lcg3 = ctx -> lcg[ 2 ];
+	PRH64S_T lcg4 = ctx -> lcg[ 3 ];
+
+	const size_t fc = PRH64S_S + ( ctx -> HashLen == PRH64S_S ? 0 :
+		ctx -> HashLen + ( ctx -> MsgLen < ctx -> HashLen * PRH64S_FUSE ?
+		(uint8_t*) HashEnd - (uint8_t*) hc : 0 ));
+
+	size_t k;
+
+	for( k = 0; k <= fc; k += PRH64S_S )
+	{
+		PRH64S_FN( &Seed1, &lcg1, hc );
+		PRH64S_FN( &Seed2, &lcg2, hc );
+		PRH64S_FN( &Seed3, &lcg3, hc );
+		PRH64S_FN( &Seed4, &lcg4, hc );
+
+		if( ++hc == HashEnd )
+		{
+			hc = (PRH64S_T*) ctx -> Hash;
+		}
+	}
+
+	uint8_t* const ho = (uint8_t*) HashOut;
+
+	for( k = 0; k < ctx -> HashLen; k += PRH64S_S )
+	{
+		PRH64S_T res = 0;
+		int i;
+
+		for( i = 0; i < 4; i++ )
+		{
+			PRH64S_FN( &Seed1, &lcg1, hc );
+			PRH64S_FN( &Seed2, &lcg2, hc );
+			PRH64S_FN( &Seed3, &lcg3, hc );
+			res ^= PRH64S_FN( &Seed4, &lcg4, hc );
+
+			if( ++hc == HashEnd )
+			{
+				hc = (PRH64S_T*) ctx -> Hash;
+			}
+		}
+
+		res = PRH64S_EC( res );
+		memcpy( ho + k, &res, PRH64S_S );
+	}
+
+	memset( ctx, 0, sizeof( PRVHASH64S_CTX ));
+}
+
+/**
+ * This function calculates the "prvhash64s" hash of the specified message in
+ * the "oneshot" mode, with default seed settings, without using streaming
+ * capabilities.
+ *
+ * @param Msg The message to produce a hash from. The alignment of this
+ * pointer is unimportant.
+ * @param MsgLen Message's length, in bytes.
+ * @param[out] Hash The hash buffer, length = HashLen. The address alignment
+ * of this buffer is unimportant.
+ * @param HashLen The required hash length, in bytes; should be >= PRH64S_S,
+ * in increments of PRH64S_S. Should not exceed PRH64S_MAX.
+ */
+
+static inline void prvhash64s_oneshot( const void* const Msg,
+	const size_t MsgLen, void* const Hash, const size_t HashLen )
+{
+	PRVHASH64S_CTX ctx;
+
+	prvhash64s_init( &ctx, HashLen, 0 );
+	prvhash64s_update( &ctx, Msg, MsgLen );
+	prvhash64s_final( &ctx, Hash );
+}
+
+#endif // PRVHASH64S_INCLUDED

prvhash.mod/prvhash/prvhash_core.h

@@ -0,0 +1,327 @@
+/**
+ * prvhash_core.h version 4.3.2
+ *
+ * The inclusion file for the "prvhash_core*" PRVHASH core functions for
+ * various state variable sizes. Also includes several auxiliary functions and
+ * macros for endianness-correction.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ * E-mail: [email protected] or [email protected]
+ *
+ * License
+ *
+ * Copyright (c) 2020-2023 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#ifndef PRVHASH_CORE_INCLUDED
+#define PRVHASH_CORE_INCLUDED
+
+#include <stdint.h>
+#include <string.h>
+
+#define PRVHASH_INIT_COUNT 5 // Common number of initialization rounds.
+
+// Macro that denotes availability of required GCC-style built-in functions.
+
+#if defined( __GNUC__ ) || defined( __clang__ ) || \
+	defined( __IBMC__ ) || defined( __IBMCPP__ ) || defined( __COMPCERT__ )
+
+	#define PRVHASH_GCC_BUILTINS
+
+#endif // GCC built-ins.
+
+// Macro to force code inlining.
+
+#if defined( PRVHASH_GCC_BUILTINS )
+
+	#define PRVHASH_INLINE inline __attribute__((always_inline))
+
+#elif defined( _MSC_VER )
+
+	#define PRVHASH_INLINE inline __forceinline
+
+#else // defined( _MSC_VER )
+
+	#define PRVHASH_INLINE inline
+
+#endif // defined( _MSC_VER )
+
+/**
+ * This function runs a single PRVHASH random number generation round. This
+ * function can be used both as a hash generator and as a general-purpose
+ * random number generator. In either case, it is advisable to initially run
+ * this function 5 times (independent of state variable's size), before using
+ * its random output, to neutralize any possible oddities of state variables'
+ * initial values (including zero values). Note that after such
+ * initialization, any further "strange" or zero values in the hashword array
+ * do not have any influence over the quality of the output (since they get
+ * mixed with the Seed that already became uniformly-random).
+ *
+ * To generate hashes, the "Seed" and "lcg" variables should be simultaneously
+ * XORed with the same entropy input, prior to calling this function.
+ * Additionally, the "Seed" can be XORed with a good-quality uniformly-random
+ * entropy (including output of another PRVHASH system): this is called
+ * "daisy-chaining", it does not interfere with hashing.
+ *
+ * @param[in,out] Seed0 The current "Seed" value. Can be initialized to any
+ * value.
+ * @param[in,out] lcg0 The current "lcg" value. Can be initialized to any
+ * value.
+ * @param[in,out] Hash0 Current hash word in a hash word array.
+ * @return Current random value.
+ */
+
+static PRVHASH_INLINE uint64_t prvhash_core64( uint64_t* const Seed0,
+	uint64_t* const lcg0, uint64_t* const Hash0 )
+{
+	uint64_t Seed = *Seed0; uint64_t lcg = *lcg0; uint64_t Hash = *Hash0;
+
+	Seed *= lcg * 2 + 1;
+	const uint64_t rs = Seed >> 32 | Seed << 32;
+	Hash += rs + 0xAAAAAAAAAAAAAAAA;
+	lcg += Seed + 0x5555555555555555;
+	Seed ^= Hash;
+	const uint64_t out = lcg ^ rs;
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+static PRVHASH_INLINE uint32_t prvhash_core32( uint32_t* const Seed0,
+	uint32_t* const lcg0, uint32_t* const Hash0 )
+{
+	uint32_t Seed = *Seed0; uint32_t lcg = *lcg0; uint32_t Hash = *Hash0;
+
+	Seed *= lcg * 2 + 1;
+	const uint32_t rs = Seed >> 16 | Seed << 16;
+	Hash += rs + 0xAAAAAAAA;
+	lcg += Seed + 0x55555555;
+	Seed ^= Hash;
+	const uint32_t out = lcg ^ rs;
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+static PRVHASH_INLINE uint16_t prvhash_core16( uint16_t* const Seed0,
+	uint16_t* const lcg0, uint16_t* const Hash0 )
+{
+	uint16_t Seed = *Seed0; uint16_t lcg = *lcg0; uint16_t Hash = *Hash0;
+
+	Seed *= (uint16_t) ( lcg * 2 + 1 );
+	const uint16_t rs = (uint16_t) ( Seed >> 8 | Seed << 8 );
+	Hash += (uint16_t) ( rs + 0xAAAA );
+	lcg += (uint16_t) ( Seed + 0x5555 );
+	Seed ^= Hash;
+	const uint16_t out = (uint16_t) ( lcg ^ rs );
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+static PRVHASH_INLINE uint8_t prvhash_core8( uint8_t* const Seed0,
+	uint8_t* const lcg0, uint8_t* const Hash0 )
+{
+	uint8_t Seed = *Seed0; uint8_t lcg = *lcg0; uint8_t Hash = *Hash0;
+
+	Seed *= (uint8_t) ( lcg * 2 + 1 );
+	const uint8_t rs = (uint8_t) ( Seed >> 4 | Seed << 4 );
+	Hash += (uint8_t) ( rs + 0xAA );
+	lcg += (uint8_t) ( Seed + 0x55 );
+	Seed ^= Hash;
+	const uint8_t out = (uint8_t) ( lcg ^ rs );
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+static PRVHASH_INLINE uint8_t prvhash_core4( uint8_t* const Seed0,
+	uint8_t* const lcg0, uint8_t* const Hash0 )
+{
+	uint8_t Seed = *Seed0; uint8_t lcg = *lcg0; uint8_t Hash = *Hash0;
+
+	Seed *= (uint8_t) ( lcg * 2 + 1 );
+	Seed &= 15;
+	const uint8_t rs = (uint8_t) (( Seed >> 2 | Seed << 2 ) & 15 );
+	Hash += (uint8_t) ( rs + 0xA );
+	Hash &= 15;
+	lcg += (uint8_t) ( Seed + 0x5 );
+	lcg &= 15;
+	Seed ^= Hash;
+	const uint8_t out = (uint8_t) ( lcg ^ rs );
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+static PRVHASH_INLINE uint8_t prvhash_core2( uint8_t* const Seed0,
+	uint8_t* const lcg0, uint8_t* const Hash0 )
+{
+	uint8_t Seed = *Seed0; uint8_t lcg = *lcg0; uint8_t Hash = *Hash0;
+
+	Seed *= (uint8_t) ( lcg * 2 + 1 );
+	Seed &= 3;
+	const uint8_t rs = (uint8_t) (( Seed >> 1 | Seed << 1 ) & 3 );
+	Hash += (uint8_t) ( rs + 0x2 );
+	Hash &= 3;
+	lcg += (uint8_t) ( Seed + 0x1 );
+	lcg &= 3;
+	Seed ^= Hash;
+	const uint8_t out = (uint8_t) ( lcg ^ rs );
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+#if defined( __SIZEOF_INT128__ )
+
+static PRVHASH_INLINE unsigned __int128 prvhash_core128(
+	unsigned __int128* const Seed0, unsigned __int128* const lcg0,
+	unsigned __int128* const Hash0 )
+{
+	unsigned __int128 Seed = *Seed0; unsigned __int128 lcg = *lcg0;
+	unsigned __int128 Hash = *Hash0;
+
+	Seed *= lcg * 2 + 1;
+	const unsigned __int128 rs = Seed >> 64 | Seed << 64;
+	Hash += rs +
+		( 0xAAAAAAAAAAAAAAAA | (unsigned __int128) 0xAAAAAAAAAAAAAAAA << 64 );
+
+	lcg += Seed +
+		( 0x5555555555555555 | (unsigned __int128) 0x5555555555555555 << 64 );
+
+	Seed ^= Hash;
+	const unsigned __int128 out = lcg ^ rs;
+
+	*Seed0 = Seed; *lcg0 = lcg; *Hash0 = Hash;
+
+	return( out );
+}
+
+#endif // defined( __SIZEOF_INT128__ )
+
+// Endianness definition macro, can be used as a logical constant.
+
+#if defined( __LITTLE_ENDIAN__ ) || defined( __LITTLE_ENDIAN ) || \
+	defined( _LITTLE_ENDIAN ) || defined( _WIN32 ) || defined( i386 ) || \
+	defined( __i386 ) || defined( __i386__ ) || defined( __x86_64__ ) || \
+	( defined( __BYTE_ORDER__ ) && __BYTE_ORDER__ == __ORDER_LITTLE_ENDIAN__ )
+
+	#define PRVHASH_LITTLE_ENDIAN 1
+
+#elif defined( __BIG_ENDIAN__ ) || defined( __BIG_ENDIAN ) || \
+	defined( _BIG_ENDIAN ) || defined( __SYSC_ZARCH__ ) || \
+	defined( __zarch__ ) || defined( __s390x__ ) || defined( __sparc ) || \
+	defined( __sparc__ ) || \
+	( defined( __BYTE_ORDER__ ) && __BYTE_ORDER__ == __ORDER_BIG_ENDIAN__ )
+
+	#define PRVHASH_LITTLE_ENDIAN 0
+
+#else // defined( __BIG_ENDIAN__ )
+
+	#warning PRVHASH: cannot determine endianness, assuming little-endian.
+
+	#define PRVHASH_LITTLE_ENDIAN 1
+
+#endif // defined( __BIG_ENDIAN__ )
+
+// Macros that apply byte-swapping, used for endianness-correction.
+
+#if PRVHASH_LITTLE_ENDIAN
+
+	#define PRVHASH_EC32( v ) ( v )
+	#define PRVHASH_EC64( v ) ( v )
+
+#else // PRVHASH_LITTLE_ENDIAN
+
+	#if defined( PRVHASH_GCC_BUILTINS )
+
+		#define PRVHASH_EC32( v ) __builtin_bswap32( v )
+		#define PRVHASH_EC64( v ) __builtin_bswap64( v )
+
+	#elif defined( _MSC_VER )
+
+		#include <intrin.h>
+
+		#define PRVHASH_EC32( v ) _byteswap_ulong( v )
+		#define PRVHASH_EC64( v ) _byteswap_uint64( v )
+
+	#else // defined( _MSC_VER )
+
+		#define PRVHASH_EC32( v ) ( \
+			( v & 0xFF000000 ) >> 24 | \
+			( v & 0x00FF0000 ) >> 8 | \
+			( v & 0x0000FF00 ) << 8 | \
+			( v & 0x000000FF ) << 24 )
+
+		#define PRVHASH_EC64( v ) ( \
+			( v & 0xFF00000000000000 ) >> 56 | \
+			( v & 0x00FF000000000000 ) >> 40 | \
+			( v & 0x0000FF0000000000 ) >> 24 | \
+			( v & 0x000000FF00000000 ) >> 8 | \
+			( v & 0x00000000FF000000 ) << 8 | \
+			( v & 0x0000000000FF0000 ) << 24 | \
+			( v & 0x000000000000FF00 ) << 40 | \
+			( v & 0x00000000000000FF ) << 56 )
+
+	#endif // defined( _MSC_VER )
+
+#endif // PRVHASH_LITTLE_ENDIAN
+
+/**
+ * An auxiliary function that returns an unsigned 32-bit value created out of
+ * individual bytes in a buffer. This function is used to convert endianness
+ * of supplied 32-bit unsigned values, and to avoid unaligned memory accesses.
+ *
+ * @param p 4-byte buffer. Alignment is unimportant.
+ */
+
+static PRVHASH_INLINE uint32_t prvhash_lu32ec( const uint8_t* const p )
+{
+	uint32_t v;
+	memcpy( &v, p, 4 );
+
+	return( PRVHASH_EC32( v ));
+}
+
+/**
+ * An auxiliary function that returns an unsigned 64-bit value created out of
+ * individual bytes in a buffer. This function is used to convert endianness
+ * of supplied 64-bit unsigned values, and to avoid unaligned memory accesses.
+ *
+ * @param p 8-byte buffer. Alignment is unimportant.
+ */
+
+static PRVHASH_INLINE uint64_t prvhash_lu64ec( const uint8_t* const p )
+{
+	uint64_t v;
+	memcpy( &v, p, 8 );
+
+	return( PRVHASH_EC64( v ));
+}
+
+#endif // PRVHASH_CORE_INCLUDED

prvhash.mod/prvhash/prvrng.h

@@ -0,0 +1,259 @@
+/**
+ * prvrng.h version 4.3.2
+ *
+ * The inclusion file for the "prvrng" entropy pseudo-random number generator.
+ * This is mostly an example PRNG that demonstrates use of infrequent external
+ * entropy injections in the course of random number generation.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ *
+ * License
+ *
+ * Copyright (c) 2020-2021 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+//$ lib "win*|AdvAPI32"
+
+#ifndef PRVRNG_INCLUDED
+#define PRVRNG_INCLUDED
+
+#include <stdio.h>
+
+#if defined( _WIN32 )
+	#include <windows.h>
+	#include <wincrypt.h>
+#else // defined( _WIN32 )
+	#define PRVRNG_UNIX 1
+#endif // defined( _WIN32 )
+
+#include "prvhash_core.h"
+
+/**
+ * prvrng context structure.
+ */
+
+#define PRVRNG_FUSE_COUNT 2 // PRNG fusing.
+#define PRVRNG_HASH_COUNT 16 // Hashwords in a hasharray.
+
+typedef struct
+{
+	#if defined( PRVRNG_UNIX )
+		FILE* f; ///< /dev/random file.
+	#else // defined( PRVRNG_UNIX )
+		HCRYPTPROV prov; ///< Crypt provider (for Windows).
+	#endif // defined( PRVRNG_UNIX )
+
+	uint64_t Seed[ PRVRNG_FUSE_COUNT ]; ///< Current Seed values.
+	uint64_t lcg[ PRVRNG_FUSE_COUNT ]; ///< Current lcg values.
+	uint64_t Hash[ PRVRNG_HASH_COUNT ]; ///< Current hash values.
+	size_t HashPos; ///< Position within the Hash array.
+	int EntCtr; ///< Bytes remaining before entropy is injected.
+	size_t OutLeft; ///< Bytes left in LastOut.
+	uint64_t LastOut; ///< Previously generated output.
+} PRVRNG_CTX;
+
+/**
+ * Internal function returns a "true" entropy value. This is simulated
+ * by obtaining a byte from "/dev/random" or Windows' CryptGenRandom().
+ *
+ * @param ctx Pointer to the context structure.
+ * @param c The number of bytes to return, 1 to 8.
+ */
+
+static inline uint64_t prvrng_get_entropy( PRVRNG_CTX* const ctx,
+	const size_t c )
+{
+	uint8_t val[ 8 ];
+	memset( val, 0, sizeof( val ));
+
+	#if defined( PRVRNG_UNIX )
+
+		fread( val, 1, c, ctx -> f );
+
+	#else // defined( PRVRNG_UNIX )
+
+		CryptGenRandom( ctx -> prov, (DWORD) c, val );
+
+	#endif // defined( PRVRNG_UNIX )
+
+	return( prvhash_lu64ec( val ));
+}
+
+/**
+ * Function generates the next random 8-bit number.
+ *
+ * @param ctx Pointer to the context structure.
+ */
+
+static inline uint8_t prvrng_gen64p2( PRVRNG_CTX* const ctx )
+{
+	if( ctx -> OutLeft == 0 )
+	{
+		if( ctx -> EntCtr == 0 )
+		{
+			const uint16_t v = (uint16_t) prvrng_get_entropy( ctx, 2 );
+			ctx -> EntCtr = ( v & 0xFF ) + 1;
+
+			const uint64_t ent = ( v >> 8 ) + 1;
+			ctx -> Seed[ 0 ] ^= ent;
+			ctx -> lcg[ 0 ] ^= ent;
+		}
+
+		uint64_t rv = 0;
+		int k;
+
+		for( k = 0; k < 2; k++ )
+		{
+			uint64_t* const Hash = ctx -> Hash + ctx -> HashPos;
+			int i;
+
+			for( i = 0; i < PRVRNG_FUSE_COUNT - 1; i++ )
+			{
+				prvhash_core64( &ctx -> Seed[ i ], &ctx -> lcg[ i ], Hash );
+			}
+
+			rv ^= prvhash_core64( &ctx -> Seed[ i ], &ctx -> lcg[ i ], Hash );
+
+			if( ++ctx -> HashPos == PRVRNG_HASH_COUNT )
+			{
+				ctx -> HashPos = 0;
+			}
+		}
+
+		ctx -> LastOut = rv;
+		ctx -> OutLeft = sizeof( ctx -> LastOut );
+		ctx -> EntCtr--;
+	}
+
+	const uint8_t r = (uint8_t) ctx -> LastOut;
+	ctx -> LastOut >>= 8;
+	ctx -> OutLeft--;
+
+	return( r );
+}
+
+/**
+ * Function initalizes the entropy PRNG context. It also seeds the generator
+ * with the initial entropy.
+ *
+ * @param ctx Pointer to the context structure.
+ * @return 0 if failed.
+ */
+
+static inline int prvrng_init64p2( PRVRNG_CTX* const ctx )
+{
+	#if defined( PRVRNG_UNIX )
+
+		ctx -> f = fopen( "/dev/random", "rb" );
+
+		if( ctx -> f == 0 )
+		{
+			return( 0 );
+		}
+
+	#else // defined( PRVRNG_UNIX )
+
+		if( !CryptAcquireContext( &ctx -> prov, 0, 0, PROV_RSA_FULL,
+			CRYPT_VERIFYCONTEXT ))
+		{
+			return( 0 );
+		}
+
+	#endif // defined( PRVRNG_UNIX )
+
+	int i;
+
+	for( i = 0; i < PRVRNG_FUSE_COUNT; i++ )
+	{
+		ctx -> Seed[ i ] = prvrng_get_entropy( ctx, sizeof( uint64_t ));
+		ctx -> lcg[ i ] = prvrng_get_entropy( ctx, sizeof( uint64_t ));
+	}
+
+	for( i = 0; i < PRVRNG_HASH_COUNT; i++ )
+	{
+		ctx -> Hash[ i ] = prvrng_get_entropy( ctx, sizeof( uint64_t ));
+	}
+
+	ctx -> HashPos = 0;
+	ctx -> EntCtr = 0;
+	ctx -> OutLeft = 0;
+	ctx -> LastOut = 0;
+
+	int k;
+
+	for( k = 0; k < PRVRNG_HASH_COUNT; k++ )
+	{
+		uint64_t* const Hash = ctx -> Hash + k;
+		int i;
+
+		for( i = 0; i < PRVRNG_FUSE_COUNT; i++ )
+		{
+			prvhash_core64( &ctx -> Seed[ i ], &ctx -> lcg[ i ], Hash );
+		}
+	}
+
+	return( 1 );
+}
+
+/**
+ * Function deinitializes the PRNG, for 32-bit hash.
+ *
+ * @param ctx Pointer to the context structure.
+ */
+
+static inline void prvrng_final64p2( PRVRNG_CTX* const ctx )
+{
+	#if defined( PRVRNG_UNIX )
+
+		fclose( ctx -> f );
+
+	#else // defined( PRVRNG_UNIX )
+
+		CryptReleaseContext( ctx -> prov, 0 );
+
+	#endif // defined( PRVRNG_UNIX )
+}
+
+/**
+ * A test function for "prvrng", 32-bit hash-based. Prints 16 random bytes.
+ */
+
+static inline void prvrng_test64p2()
+{
+	PRVRNG_CTX ctx;
+
+	if( !prvrng_init64p2( &ctx ))
+	{
+		printf( "Cannot obtain the entropy source!\n" );
+		return;
+	}
+
+	int i;
+
+	for( i = 0; i < 16; i++ )
+	{
+		printf( "%i\n", (int) prvrng_gen64p2( &ctx ));
+	}
+
+	prvrng_final64p2( &ctx );
+}
+
+#endif // PRVRNG_INCLUDED

prvhash.mod/prvhash/t642_sat.py

@@ -0,0 +1,247 @@
+# tango642 4.3.9 SAT solving simulation -
+# finds a key specified in seed_i and hcv[].
+# requires autosat from https://github.com/petersn/autosat
+# and python-sat
+#
+# use "time python t642_sat.py" to measure solving time.
+# increase "bits" (an even value) to estimate solving complexity. "bits=64"
+# corresponds to real tango642 variable size. a minimal reasonable "bits"
+# value is 6; lower values solve instantly. base exponential time increase can
+# be assessed by setting hci=0 and incrementally assigning various "bits"
+# values. note that the SAT solver may have to consider most of the system
+# anyway, so a time difference between various "hci" values may not be
+# pronounced. the time exponent dependence on "hci" itself depends on "bits"
+# asymptotically, with higher "bits" values producing a more linear "hci*bits"
+# exponent.
+
+import autosat
+
+##### simulation parameters
+
+bits = 6 # state variable size
+hci = 2 # number of keyed hash elements in use (key length-1)
+ivlen = 4 # nonce vector length
+
+seed_i = 4 # keyed prng init (key value 1)
+hcv = [3,14,3,13,14,4,2,15,2,5,6,11,9,1,11,5,8,6,10,7,5,6,3,10,3,0,2,9,9,12,15,11] # key values
+iv = [15,9,4,6] # nonce vector
+
+hc = 16 # keyed hash array length
+fc = 15 # firewall prng init length
+num_obs = 16 # number of observations to use for solving (*4)
+
+#####
+
+def inibits(inst,l,ini):
+    result = []
+    for i in range(l):
+        if( (ini>>i)&1 ):
+            v=True
+        else:
+            v=False
+        result.append(inst.get_constant(v))
+    return result
+
[email protected]
+def full_adder(a, b, carry_in):
+    r = a + b + carry_in
+    return r & 1, (r & 2) >> 1
+
+def add(a, b):
+    assert len(a) == len(b)
+    carry = False
+    result = []
+    for a_bit, b_bit in zip(a, b):
+        sum_bit, carry = full_adder(a_bit, b_bit, carry)
+        result.append(sum_bit)
+    return result
+
+def xor(a, b):
+    assert len(a) == len(b)
+    return [i ^ j for i, j in zip(a, b)]
+
+def and_(a, b):
+    assert len(a) == len(b)
+    return [i & j for i, j in zip(a, b)]
+
+def mul(a, b):
+    assert len(a) == len(b)
+    result = [a[0] & bit for bit in b]
+    for i in range(1, len(a)):
+        addend = [a[i] & bit for bit in b[:-i]]
+        result[i:] = add(result[i:], addend)
+    return result
+
+obs = [] # observations
+bits2 = bits>>1
+bmask = (1<<bits)-1
+rawbits5 = 0
+rawbitsA = 0
+
+for i in range(bits2):
+    rawbits5 <<= 2
+    rawbits5 |= 0x1
+    rawbitsA <<= 2
+    rawbitsA |= 0x2
+
+def prvhash_core_calc(seed, lcg, h):
+    seed = seed * ( lcg * 2 + 1 )
+    seed &= bmask
+    rs = seed>>bits2 | seed<<bits2
+    rs &= bmask
+    h += rs + rawbitsA
+    h &= bmask
+    lcg += seed + rawbits5
+    lcg &= bmask
+    seed ^= h
+    out = lcg ^ rs
+    return seed, lcg, h, out
+
+# calculate real outputs
+
+calc_seed = seed_i&bmask
+calc_lcg = 0
+calc_h = []
+calc_seed1 = 0
+calc_lcg1 = 0
+calc_seed2 = 0
+calc_lcg2 = 0
+calc_seed3 = 0
+calc_lcg3 = 0
+calc_seed4 = 0
+calc_lcg4 = 0
+calc_h2 = [0,0,0,0,0]
+
+for i in range(hc):
+    if(i < hci):
+        calc_h.append(hcv[i]&bmask)
+    else:
+        calc_h.append(0)
+
+calc_x = 0
+calc_x2 = 0
+ivpos = 0
+
+for i in range(5):
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+
+for i in range(hc):
+    if((i&1)==1 and ivpos < ivlen):
+        calc_seed ^= iv[ivpos]&bmask
+        calc_lcg ^= iv[ivpos]&bmask
+        ivpos += 1
+
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+    calc_x += 1
+
+for i in range(hc+1):
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+    calc_x += 1
+
+for i in range(fc+num_obs):
+    calc_seed, calc_lcg, calc_h[calc_x%hc], out1 = prvhash_core_calc(calc_seed, calc_lcg, calc_h[calc_x%hc])
+    calc_x += 1
+
+    calc_seed4 ^= out1
+    calc_seed1, calc_lcg1, calc_h2[(calc_x2+0)%5], outf1 = prvhash_core_calc(calc_seed1, calc_lcg1, calc_h2[(calc_x2+0)%5])
+    calc_seed2, calc_lcg2, calc_h2[(calc_x2+1)%5], outf2 = prvhash_core_calc(calc_seed2, calc_lcg2, calc_h2[(calc_x2+1)%5])
+    calc_seed3, calc_lcg3, calc_h2[(calc_x2+2)%5], outf3 = prvhash_core_calc(calc_seed3, calc_lcg3, calc_h2[(calc_x2+2)%5])
+    calc_seed4, calc_lcg4, calc_h2[(calc_x2+3)%5], outf4 = prvhash_core_calc(calc_seed4, calc_lcg4, calc_h2[(calc_x2+3)%5])
+    calc_x2 += 1
+
+    if(i>=fc):
+        obs.append(outf1)
+        obs.append(outf2)
+        obs.append(outf3)
+        obs.append(outf4)
+
+print("----")
+
+# solve initial state
+
+inst = autosat.Instance()
+
+BITR5 = inibits(inst, bits, rawbits5)
+BITRA = inibits(inst, bits, rawbitsA)
+
+def prvhash_core_sat(seed, lcg, h):
+    seed = mul(seed, [True] + lcg[:-1])
+    rs = seed[bits2:] + seed[:bits2]
+    h = add(h, add(rs, BITRA))
+    lcg = add(lcg, add(seed, BITR5))
+    seed = xor(seed, h)
+    out = xor(lcg, rs)
+    return seed, lcg, h, out
+
+start_seed = inst.new_vars(bits)
+start_h = []
+
+seed = start_seed[:]
+h = []
+
+for i in range(hc):
+    if(i < hci):
+        start_h.append(inst.new_vars(bits))
+        h.append(start_h[i][:])
+    else:
+        h.append(inibits(inst, bits, 0))
+
+lcg = inibits(inst, bits, 0)
+seed1 = inibits(inst, bits, 0)
+lcg1 = inibits(inst, bits, 0)
+seed2 = inibits(inst, bits, 0)
+lcg2 = inibits(inst, bits, 0)
+seed3 = inibits(inst, bits, 0)
+lcg3 = inibits(inst, bits, 0)
+seed4 = inibits(inst, bits, 0)
+lcg4 = inibits(inst, bits, 0)
+h2 = [inibits(inst, bits, 0),inibits(inst, bits, 0),inibits(inst, bits, 0),inibits(inst, bits, 0),inibits(inst, bits, 0)]
+
+x = 0
+x2 = 0
+ivpos = 0
+
+for k in range(5):
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+
+for k in range(hc):
+    if((k&1)==1 and ivpos < ivlen):
+        seed = xor(seed, inibits(inst,bits,iv[ivpos]))
+        lcg = xor(lcg, inibits(inst,bits,iv[ivpos]))
+        ivpos += 1
+
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+    x += 1
+
+for k in range(hc+1):
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+    x += 1
+
+for k in range(fc+num_obs):
+    seed, lcg, h[x % hc], out1 = prvhash_core_sat(seed, lcg, h[x % hc])
+    x += 1
+
+    seed4 = xor(seed4, out1)
+    seed1, lcg1, h2[(x2+0)%5], outf1 = prvhash_core_sat(seed1, lcg1, h2[(x2+0)%5])
+    seed2, lcg2, h2[(x2+1)%5], outf2 = prvhash_core_sat(seed2, lcg2, h2[(x2+1)%5])
+    seed3, lcg3, h2[(x2+2)%5], outf3 = prvhash_core_sat(seed3, lcg3, h2[(x2+2)%5])
+    seed4, lcg4, h2[(x2+3)%5], outf4 = prvhash_core_sat(seed4, lcg4, h2[(x2+3)%5])
+    x2 += 1
+
+    if(k>=fc):
+        for i, b in enumerate(outf1):
+            b.make_equal(bool((obs[(k-fc)*4+0] >> i) & 1))
+        for i, b in enumerate(outf2):
+            b.make_equal(bool((obs[(k-fc)*4+1] >> i) & 1))
+        for i, b in enumerate(outf3):
+            b.make_equal(bool((obs[(k-fc)*4+2] >> i) & 1))
+        for i, b in enumerate(outf4):
+            b.make_equal(bool((obs[(k-fc)*4+3] >> i) & 1))
+
+model = inst.solve(solver_name="Glucose3",decode_model=False)
+#print(model)
+
+print("seed = %4i (%4i)" % (autosat.decode_number(start_seed, model), (seed_i&bmask)))
+
+for i in range(hci):
+    print("hash = %4i (%4i)" % (autosat.decode_number(start_h[i], model), (hcv[i]&bmask)))

prvhash.mod/prvhash/tango642.h

@@ -0,0 +1,404 @@
+/**
+ * tango642.h version 4.3.9
+ *
+ * The inclusion file for the "tango642" PRVHASH PRNG-based streamed XOR
+ * function.
+ *
+ * Description is available at https://github.com/avaneev/prvhash
+ *
+ * License
+ *
+ * Copyright (c) 2020-2023 Aleksey Vaneev
+ *
+ * Permission is hereby granted, free of charge, to any person obtaining a
+ * copy of this software and associated documentation files (the "Software"),
+ * to deal in the Software without restriction, including without limitation
+ * the rights to use, copy, modify, merge, publish, distribute, sublicense,
+ * and/or sell copies of the Software, and to permit persons to whom the
+ * Software is furnished to do so, subject to the following conditions:
+ *
+ * The above copyright notice and this permission notice shall be included in
+ * all copies or substantial portions of the Software.
+ *
+ * THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+ * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+ * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+ * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+ * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
+ * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
+ * DEALINGS IN THE SOFTWARE.
+ */
+
+#ifndef TANGO642_INCLUDED
+#define TANGO642_INCLUDED
+
+#include "prvhash_core.h"
+
+#define TANGO642_T uint64_t // PRVHASH state variable type.
+#define TANGO642_S sizeof( TANGO642_T ) // State variable type's size.
+#define TANGO642_S_2 ( TANGO642_S * 2 )
+#define TANGO642_HASH_COUNT 16 // Hashwords in keyed PRNG (power-of-2).
+#define TANGO642_HASH_SIZE ( TANGO642_HASH_COUNT * TANGO642_S )
+#define TANGO642_HASH_MASK ( TANGO642_HASH_SIZE - 1 )
+#define TANGO642_PAR 4 // Firewalling "parallel PRNG" size.
+#define TANGO642_FN prvhash_core64 // PRVHASH core function name.
+#define TANGO642_LUEC prvhash_lu64ec // Unsigned value EC load function.
+#define TANGO642_EC PRVHASH_EC64 // Value EC function.
+#define TANGO642_SH( v1, v2, v3, v4, v5 ) \
+	{ TANGO642_T t = v1; v1 = v2; v2 = v3; v3 = v4; v4 = v5; v5 = t; }
+	// 5-value shift macro.
+
+/**
+ * tango642 context structure, can be placed on stack. On systems where this
+ * is relevant, the structure should be aligned to TANGO642_S bytes.
+ */
+
+typedef struct
+{
+	TANGO642_T Seed; ///< Keyed PRNG Seed value.
+	TANGO642_T lcg; ///< Keyed PRNG lcg value.
+	TANGO642_T Hash[ TANGO642_HASH_COUNT ]; ///< Keyed PRNG hash values.
+	TANGO642_T SeedF[ TANGO642_PAR ]; ///< Firewalling PRNG Seed values.
+	TANGO642_T lcgF[ TANGO642_PAR ]; ///< Firewalling PRNG lcg values.
+	TANGO642_T HashF[ TANGO642_PAR + 1 ]; ///< Firewalling PRNG hash values.
+	TANGO642_T RndBytes[ TANGO642_PAR ]; ///< The leftover random output.
+	size_t RndLeft[ TANGO642_PAR ]; ///< The number of bytes left in RndBytes.
+	size_t RndPos; ///< Position within the RndLeft array.
+	size_t HashPos; ///< Keyed PRNG hash array position, in bytes.
+} TANGO642_CTX;
+
+/**
+ * This function initializes the "tango642" structure. After the session, the
+ * tango642_final() function should be called.
+ *
+ * Note that this function can be also used as a "conditioning" function for
+ * the specified "key" and "iv" values, to minimize overhead if "iv" values
+ * are pre-generated and cached. In this case, the initialized context
+ * structure can be stored as a whole, and used as a substitute for key+iv
+ * pair.
+ *
+ * When "keylen+ivlen" is larger than 1104 bits, there can be theoretical
+ * "key+iv" collisions: such collisions should not pose a security threat
+ * (negligible probability), but may be perceived as "non-ideal". However,
+ * when the "keylen" is 1024 bits long it still allows "iv" to be 64 bits
+ * long "safely".
+ *
+ * @param[out] ctx Pointer to the context structure. Should be aligned to
+ * 8 bytes.
+ * @param key0 Uniformly-random key buffer, address alignment is unimportant.
+ * @param keylen Length of "key", in bytes; should be >= 16, in increments of
+ * 8. Should not exceed 128 bytes.
+ * @param iv0 Uniformly-random "unsecure" initialization vector (nonce),
+ * address alignment is unimportant. Can be 0 if "ivlen" is also 0.
+ * @param ivlen Length of "iv", in bytes, in increments of 8; can be zero.
+ * Should not exceed 64 bytes.
+ */
+
+static inline void tango642_init( TANGO642_CTX* const ctx,
+	const void* const key0, const size_t keylen, const void* const iv0,
+	const size_t ivlen )
+{
+	const uint8_t* const key = (const uint8_t*) key0;
+	const uint8_t* const iv = (const uint8_t*) iv0;
+
+	memset( ctx, 0, sizeof( TANGO642_CTX ));
+
+	// Load a key.
+
+	TANGO642_T Seed = TANGO642_LUEC( key );
+	TANGO642_T lcg = 0;
+
+	uint8_t* const ha = (uint8_t*) ctx -> Hash;
+	uint8_t* ha2 = ha - TANGO642_S;
+	size_t i;
+
+	for( i = TANGO642_S; i < keylen; i += TANGO642_S )
+	{
+		*(TANGO642_T*) ( ha2 + i ) = TANGO642_LUEC( key + i );
+	}
+
+	// Initialize keyed PRNG.
+
+	for( i = 0; i < PRVHASH_INIT_COUNT; i++ )
+	{
+		TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ha );
+	}
+
+	// Input "iv" as external unstructured entropy.
+
+	ha2 = ha;
+
+	for( i = 0; i < ivlen; i += TANGO642_S )
+	{
+		TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ha2 );
+
+		const TANGO642_T v = TANGO642_LUEC( iv + i );
+
+		Seed ^= v;
+		lcg ^= v;
+
+		TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ( ha2 + TANGO642_S ));
+
+		ha2 += TANGO642_S_2;
+	}
+
+	for( i = i * 2; i < TANGO642_HASH_SIZE; i += TANGO642_S )
+	{
+		TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ( ha + i ));
+	}
+
+	// Eliminate traces of input entropy, like it is done in hashing.
+
+	for( i = 0; i < TANGO642_HASH_SIZE; i += TANGO642_S )
+	{
+		TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ( ha + i ));
+	}
+
+	TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ha );
+
+	// Initialize firewalling PRNG, making sure each lcg and hash value
+	// receives keyed entropy thrice, or otherwise a further keyed entropy
+	// input helps to reveal the key. Such entropy accumulation is the essence
+	// of "firewalling".
+
+	TANGO642_T SeedF1 = ctx -> SeedF[ 0 ];
+	TANGO642_T SeedF2 = ctx -> SeedF[ 1 ];
+	TANGO642_T SeedF3 = ctx -> SeedF[ 2 ];
+	TANGO642_T SeedF4 = ctx -> SeedF[ 3 ];
+	TANGO642_T lcgF1 = ctx -> lcgF[ 0 ];
+	TANGO642_T lcgF2 = ctx -> lcgF[ 1 ];
+	TANGO642_T lcgF3 = ctx -> lcgF[ 2 ];
+	TANGO642_T lcgF4 = ctx -> lcgF[ 3 ];
+	TANGO642_T HashF1 = ctx -> HashF[ 0 ];
+	TANGO642_T HashF2 = ctx -> HashF[ 1 ];
+	TANGO642_T HashF3 = ctx -> HashF[ 2 ];
+	TANGO642_T HashF4 = ctx -> HashF[ 3 ];
+	TANGO642_T HashF5 = ctx -> HashF[ 4 ];
+
+	size_t hp = TANGO642_S;
+
+	for( i = 0; i < ( TANGO642_PAR + 1 ) * 3; i++ )
+	{
+		// Input from keyed PRNG extends PRNG period's exponent of the output.
+
+		SeedF4 ^= TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ( ha + hp ));
+		hp = ( hp + TANGO642_S ) & TANGO642_HASH_MASK;
+
+		// Parallel arrangement PRNG for efficiency.
+
+		TANGO642_FN( &SeedF1, &lcgF1, &HashF1 );
+		TANGO642_FN( &SeedF2, &lcgF2, &HashF2 );
+		TANGO642_FN( &SeedF3, &lcgF3, &HashF3 );
+		TANGO642_FN( &SeedF4, &lcgF4, &HashF4 );
+
+		TANGO642_SH( HashF1, HashF2, HashF3, HashF4, HashF5 );
+	}
+
+	ctx -> Seed = Seed;
+	ctx -> lcg = lcg;
+	ctx -> SeedF[ 0 ] = SeedF1;
+	ctx -> SeedF[ 1 ] = SeedF2;
+	ctx -> SeedF[ 2 ] = SeedF3;
+	ctx -> SeedF[ 3 ] = SeedF4;
+	ctx -> lcgF[ 0 ] = lcgF1;
+	ctx -> lcgF[ 1 ] = lcgF2;
+	ctx -> lcgF[ 2 ] = lcgF3;
+	ctx -> lcgF[ 3 ] = lcgF4;
+	ctx -> HashF[ 0 ] = HashF1;
+	ctx -> HashF[ 1 ] = HashF2;
+	ctx -> HashF[ 2 ] = HashF3;
+	ctx -> HashF[ 3 ] = HashF4;
+	ctx -> HashF[ 4 ] = HashF5;
+	ctx -> HashPos = hp;
+	ctx -> RndPos = TANGO642_PAR;
+}
+
+/**
+ * This function applies XOR operation over the specified "message" buffer.
+ * Prior to using this function, the tango642_init() function should be
+ * called.
+ *
+ * @param[in,out] ctx Pointer to the context structure.
+ * @param[in,out] msg0 Message buffer, address alignment is unimportant,
+ * can be zero if msglen is zero.
+ * @param msglen Message length, in bytes, can be zero.
+ */
+
+static inline void tango642_xor( TANGO642_CTX* const ctx, void* const msg0,
+	size_t msglen )
+{
+	uint8_t* msg = (uint8_t*) msg0;
+
+	while( 1 )
+	{
+		if( ctx -> RndPos == TANGO642_PAR )
+		{
+			TANGO642_T Seed = ctx -> Seed;
+			TANGO642_T lcg = ctx -> lcg;
+			TANGO642_T SeedF1 = ctx -> SeedF[ 0 ];
+			TANGO642_T SeedF2 = ctx -> SeedF[ 1 ];
+			TANGO642_T SeedF3 = ctx -> SeedF[ 2 ];
+			TANGO642_T SeedF4 = ctx -> SeedF[ 3 ];
+			TANGO642_T lcgF1 = ctx -> lcgF[ 0 ];
+			TANGO642_T lcgF2 = ctx -> lcgF[ 1 ];
+			TANGO642_T lcgF3 = ctx -> lcgF[ 2 ];
+			TANGO642_T lcgF4 = ctx -> lcgF[ 3 ];
+			TANGO642_T HashF1 = ctx -> HashF[ 0 ];
+			TANGO642_T HashF2 = ctx -> HashF[ 1 ];
+			TANGO642_T HashF3 = ctx -> HashF[ 2 ];
+			TANGO642_T HashF4 = ctx -> HashF[ 3 ];
+			TANGO642_T HashF5 = ctx -> HashF[ 4 ];
+			uint8_t* const ha = (uint8_t*) ctx -> Hash;
+			size_t hp = ctx -> HashPos;
+
+			while( msglen >= TANGO642_S * TANGO642_PAR )
+			{
+				SeedF4 ^= TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ( ha + hp ));
+				hp = ( hp + TANGO642_S ) & TANGO642_HASH_MASK;
+
+				TANGO642_T mx1, mx2;
+				memcpy( &mx1, msg, TANGO642_S );
+				memcpy( &mx2, msg + TANGO642_S, TANGO642_S );
+
+				mx1 ^= TANGO642_EC( TANGO642_FN( &SeedF1, &lcgF1, &HashF1 ));
+				memcpy( msg, &mx1, TANGO642_S );
+				msg += TANGO642_S;
+
+				mx2 ^= TANGO642_EC( TANGO642_FN( &SeedF2, &lcgF2, &HashF2 ));
+				memcpy( msg, &mx2, TANGO642_S );
+				msg += TANGO642_S;
+
+				TANGO642_T mx3, mx4;
+				memcpy( &mx3, msg, TANGO642_S );
+				memcpy( &mx4, msg + TANGO642_S, TANGO642_S );
+
+				mx3 ^= TANGO642_EC( TANGO642_FN( &SeedF3, &lcgF3, &HashF3 ));
+				memcpy( msg, &mx3, TANGO642_S );
+				msg += TANGO642_S;
+
+				mx4 ^= TANGO642_EC( TANGO642_FN( &SeedF4, &lcgF4, &HashF4 ));
+				memcpy( msg, &mx4, TANGO642_S );
+				msg += TANGO642_S;
+
+				TANGO642_SH( HashF1, HashF2, HashF3, HashF4, HashF5 );
+
+				msglen -= TANGO642_S * TANGO642_PAR;
+			}
+
+			SeedF4 ^= TANGO642_FN( &Seed, &lcg, (TANGO642_T*) ( ha + hp ));
+			hp = ( hp + TANGO642_S ) & TANGO642_HASH_MASK;
+
+			ctx -> RndBytes[ 0 ] = TANGO642_FN( &SeedF1, &lcgF1, &HashF1 );
+			ctx -> RndBytes[ 1 ] = TANGO642_FN( &SeedF2, &lcgF2, &HashF2 );
+			ctx -> RndBytes[ 2 ] = TANGO642_FN( &SeedF3, &lcgF3, &HashF3 );
+			ctx -> RndBytes[ 3 ] = TANGO642_FN( &SeedF4, &lcgF4, &HashF4 );
+
+			ctx -> RndLeft[ 0 ] = TANGO642_S;
+			ctx -> RndLeft[ 1 ] = TANGO642_S;
+			ctx -> RndLeft[ 2 ] = TANGO642_S;
+			ctx -> RndLeft[ 3 ] = TANGO642_S;
+			ctx -> RndPos = 0;
+
+			ctx -> Seed = Seed;
+			ctx -> lcg = lcg;
+			ctx -> SeedF[ 0 ] = SeedF1;
+			ctx -> SeedF[ 1 ] = SeedF2;
+			ctx -> SeedF[ 2 ] = SeedF3;
+			ctx -> SeedF[ 3 ] = SeedF4;
+			ctx -> lcgF[ 0 ] = lcgF1;
+			ctx -> lcgF[ 1 ] = lcgF2;
+			ctx -> lcgF[ 2 ] = lcgF3;
+			ctx -> lcgF[ 3 ] = lcgF4;
+			ctx -> HashF[ 0 ] = HashF2; // Store shifted.
+			ctx -> HashF[ 1 ] = HashF3;
+			ctx -> HashF[ 2 ] = HashF4;
+			ctx -> HashF[ 3 ] = HashF5;
+			ctx -> HashF[ 4 ] = HashF1;
+			ctx -> HashPos = hp;
+		}
+
+		size_t p = ctx -> RndPos;
+
+		while( 1 )
+		{
+			size_t rl = ctx -> RndLeft[ p ];
+
+			if( msglen < rl )
+			{
+				if( msglen != 0 )
+				{
+					TANGO642_T RndBytes = ctx -> RndBytes[ p ];
+					ctx -> RndLeft[ p ] = rl - msglen;
+
+					do
+					{
+						*msg ^= (uint8_t) RndBytes;
+						RndBytes >>= 8;
+						msg++;
+					} while( --msglen != 0 );
+
+					ctx -> RndBytes[ p ] = RndBytes;
+				}
+
+				ctx -> RndPos = p;
+				return;
+			}
+
+			TANGO642_T RndBytes = ctx -> RndBytes[ p ];
+			msglen -= rl;
+
+			do
+			{
+				*msg ^= (uint8_t) RndBytes;
+				RndBytes >>= 8;
+				msg++;
+			} while( --rl != 0 );
+
+			if( ++p == TANGO642_PAR )
+			{
+				ctx -> RndPos = p;
+				break;
+			}
+		}
+	}
+}
+
+/**
+ * Function finalizes the XOR session.
+ *
+ * @param[in,out] ctx Pointer to the context structure.
+ */
+
+static inline void tango642_final( TANGO642_CTX* const ctx )
+{
+	memset( ctx, 0, sizeof( TANGO642_CTX ));
+}
+
+/**
+ * This is a "fun concept" XOR session finalization function, to better stand
+ * yet unknown quantum-temporal-level malevolent ET challenges (then,
+ * increasing TANGO642_HASH_COUNT to some more serious numbers would be
+ * necessary).
+ *
+ * @param[in,out] ctx Pointer to the context structure.
+ */
+
+static inline void tango642_final_selfdestruct( TANGO642_CTX* const ctx )
+{
+	TANGO642_CTX pad;
+	const size_t c = sizeof( TANGO642_CTX );
+
+	memset( &pad, 0, c );
+	tango642_xor( ctx, &pad, c );
+
+	memcpy( ctx, &pad, c );
+
+	// Now needs an immediate processor's cache system sync with the main
+	// memory. Trouble if unpadded *ctx's traces remained in cache, on any
+	// core.
+
+	memset( ctx, 0, c );
+	memset( &pad, 0, c );
+}
+
+#endif // TANGO642_INCLUDED

secure.mod/doc/intro.bbdoc

@@ -0,0 +1,33 @@
+The Random.Secure module provides a robust and secure way to generate random numbers across each platform.
+This module is designed to leverage the underlying cryptographic services of each operating system,
+ensuring that the random numbers produced are high-quality.
+
+Because of this, this particular module does not provide a way to seed the random number generator.
+
+## Windows
+On Windows, Random.Secure uses the Cryptographic Application Programming Interface (CryptoAPI).
+
+Specifically, it employs the `CryptGenRandom` function, which is part of the Windows Cryptography API: Next Generation (CNG).
+This function accesses the system's cryptographic service provider to produce a stream of random bytes.
+These bytes are considered cryptographically secure, as they are generated using a random number generator (RNG) that has been seeded
+with the current system time, process ID, thread ID, and various other high-entropy sources. The use of `CryptGenRandom` ensures that the
+randomness is of high quality and the API takes care of all the complex entropy management and seed generation.
+
+## macOS
+For macOS, the Random.Secure module taps into the native Security framework, utilizing the `SecRandomCopyBytes` function.
+
+This function is a part of Apple's security best practices and provides an interface to a cryptographically secure random number generator.
+
+Unlike reading from /dev/random or /dev/urandom, which can be less efficient and direct, `SecRandomCopyBytes` ensures that the random data is
+retrieved efficiently and is of high quality. It automatically handles entropy pooling and reseeding, pulling from the same entropy sources
+that the OS itself uses for cryptographic operations.
+
+## Linux
+On Linux systems, Random.Secure reads directly from the `/dev/urandom` device file.
+
+Unlike `/dev/random`, `/dev/urandom` does not block if there is perceived to be a lack of entropy; instead, it reuses the internal pool
+to produce more pseudo-random bits. This makes `/dev/urandom` suitable for high-throughput random number generation without the risk of
+stalling the application.
+
+The module manages the file descriptor for `/dev/urandom` efficiently, opening it once and reading from it as needed,
+which avoids the overhead of repeatedly opening and closing the file.

secure.mod/examples/example_01.bmx

@@ -0,0 +1,8 @@
+SuperStrict
+
+Framework BRL.Standardio
+Import Random.Secure
+
+For Local i:Int = 0 until 30
+	Print RndDouble()
+Next

secure.mod/linux_glue.c

@@ -0,0 +1,48 @@
+/*
+Copyright (c) 2023 Bruce A Henderson
+
+This software is provided 'as-is', without any express or implied
+warranty. In no event will the authors be held liable for any damages
+arising from the use of this software.
+
+Permission is granted to anyone to use this software for any purpose,
+including commercial applications, and to alter it and redistribute it
+freely, subject to the following restrictions:
+
+   1. The origin of this software must not be misrepresented; you must not
+   claim that you wrote the original software. If you use this software
+   in a product, an acknowledgment in the product documentation would be
+   appreciated but is not required.
+
+   2. Altered source versions must be plainly marked as such, and must not be
+   misrepresented as being the original software.
+
+   3. This notice may not be removed or altered from any source
+   distribution.
+*/
+#include <stdlib.h>
+#include <fcntl.h>
+#include <unistd.h>
+#include <stdint.h>
+
+static inline double uint64_to_double(uint64_t v) {
+    return (v >> 11) * (1.0/9007199254740992.0);
+}
+
+int bmx_secure_init() {
+    return open("/dev/urandom", O_RDONLY);
+}
+
+void bmx_secure_destroy(int fd) {
+    close(fd);
+}
+
+uint64_t bmx_secure_random(int fd) {
+    uint64_t result;
+    read(fd, &result, sizeof(result));
+    return result;
+}
+
+double bmx_secure_next_double(int fd) {
+	return uint64_to_double(bmx_secure_random(fd));
+}

secure.mod/macos_glue.c

@@ -0,0 +1,37 @@
+/*
+Copyright (c) 2023 Bruce A Henderson
+
+This software is provided 'as-is', without any express or implied
+warranty. In no event will the authors be held liable for any damages
+arising from the use of this software.
+
+Permission is granted to anyone to use this software for any purpose,
+including commercial applications, and to alter it and redistribute it
+freely, subject to the following restrictions:
+
+   1. The origin of this software must not be misrepresented; you must not
+   claim that you wrote the original software. If you use this software
+   in a product, an acknowledgment in the product documentation would be
+   appreciated but is not required.
+
+   2. Altered source versions must be plainly marked as such, and must not be
+   misrepresented as being the original software.
+
+   3. This notice may not be removed or altered from any source
+   distribution.
+*/
+#include <Security/Security.h>
+
+static inline double uint64_to_double(uint64_t v) {
+	return (v >> 11) * (1.0/9007199254740992.0);
+}
+
+uint64_t bmx_secure_random() {
+    uint64_t result;
+    SecRandomCopyBytes(kSecRandomDefault, sizeof(result), (uint8_t *)&result);
+    return result;
+}
+
+double bmx_secure_next_double() {
+	return uint64_to_double(bmx_secure_random());
+}

secure.mod/secure.bmx

@@ -0,0 +1,154 @@
+' Copyright (c) 2023 Bruce A Henderson
+'
+' This software is provided 'as-is', without any express or implied
+' warranty. In no event will the authors be held liable for any damages
+' arising from the use of this software.
+'
+' Permission is granted to anyone to use this software for any purpose,
+' including commercial applications, and to alter it and redistribute it
+' freely, subject to the following restrictions:
+'
+'    1. The origin of this software must not be misrepresented; you must not
+'    claim that you wrote the original software. If you use this software
+'    in a product, an acknowledgment in the product documentation would be
+'    appreciated but is not required.
+'
+'    2. Altered source versions must be plainly marked as such, and must not be
+'    misrepresented as being the original software.
+'
+'    3. This notice may not be removed or altered from any source
+'    distribution.
+'
+SuperStrict
+
+Rem
+bbdoc: Random Numbers - Secure
+End Rem
+Module Random.Secure
+
+ModuleInfo "Version: 1.00"
+ModuleInfo "License: zlib"
+ModuleInfo "Copyright: 2023 Bruce A Henderson"
+
+Import Random.Core
+
+?macos
+	Import "-framework Security"
+	Import "macos_glue.c"
+?win32
+	Import "-ladvapi32"
+	Import "win32_glue.c"
+?linux
+	Import "linux_glue.c"
+?
+
+Type TSecureRandom Extends TRandom
+
+	Private
+
+?win32
+	Field context:ULongInt
+?linux
+	Field fd:Int
+?
+	
+	Public
+	
+	Method New()
+?win32
+		context = bmx_secure_init()
+?linux
+		fd = bmx_secure_init()
+?
+	End Method
+	
+	Method New(seed:Int)
+?win32
+		context = bmx_secure_init()
+?linux
+		fd = bmx_secure_init()
+?
+	End Method
+	
+	Method RndFloat:Float() Override
+		Return Float(RndDouble())
+	End Method
+	
+	Method RndDouble:Double() Override
+?win32
+		Return bmx_secure_next_double(context)
+?macos
+		Return bmx_secure_next_double()
+?linux
+		Return bmx_secure_next_double(fd)
+?
+	End Method
+	
+	Method Rnd:Double(minValue:Double = 1, maxValue:Double = 0) Override
+		If maxValue > minValue Return RndDouble() * (maxValue - minValue) + minValue
+		Return RndDouble() * (minValue - maxValue) + maxValue
+	End Method
+	
+	Method Rand:Int(minValue:Int, maxValue:Int = 1) Override
+		Local Range:Double = maxValue - minValue
+		If Range > 0 Return Int( bmx_secure_next_double()*(1:Double+Range) )+minValue
+		Return Int( bmx_secure_next_double()*(1:Double-Range) )+maxValue
+	End Method
+	
+	Method SeedRnd(seed:Int) Override
+	End Method
+	
+	Method RndSeed:Int() Override
+		Return 0
+	End Method
+
+	Method GetName:String() Override
+		Return "Secure"
+	End Method
+
+	Method Delete()
+?win32
+		bmx_secure_destroy(context)
+?linux
+		bmx_secure_destroy(fd)
+?
+	End Method
+End Type
+
+Private
+Type TSecureRandomFactory Extends TRandomFactory
+	
+	Method New()
+		Super.New()
+		Init()
+	End Method
+	
+	Method GetName:String()
+		Return "Secure"
+	End Method
+	
+	Method Create:TRandom(seed:Int)
+		Return New TSecureRandom()
+	End Method
+
+	Method Create:TRandom()
+		Return New TSecureRandom()
+	End Method
+		
+End Type
+
+Extern
+?macos
+	Function bmx_secure_next_double:Double()
+?win32
+	Function bmx_secure_next_double:Double(context:ULongInt)
+	Function bmx_secure_destroy(context:ULongInt)
+	Function bmx_secure_init:ULongInt()
+?linux
+	Function bmx_secure_next_double:Double(fd:Int)
+	Function bmx_secure_init:Int()
+	Function bmx_secure_destroy(fd:Int)
+?
+End Extern
+
+New TSecureRandomFactory

secure.mod/win32_glue.c

@@ -0,0 +1,49 @@
+/*
+Copyright (c) 2023 Bruce A Henderson
+
+This software is provided 'as-is', without any express or implied
+warranty. In no event will the authors be held liable for any damages
+arising from the use of this software.
+
+Permission is granted to anyone to use this software for any purpose,
+including commercial applications, and to alter it and redistribute it
+freely, subject to the following restrictions:
+
+   1. The origin of this software must not be misrepresented; you must not
+   claim that you wrote the original software. If you use this software
+   in a product, an acknowledgment in the product documentation would be
+   appreciated but is not required.
+
+   2. Altered source versions must be plainly marked as such, and must not be
+   misrepresented as being the original software.
+
+   3. This notice may not be removed or altered from any source
+   distribution.
+*/
+#include <Windows.h>
+#include <Wincrypt.h>
+#include <stdint.h>
+
+static inline double uint64_to_double(uint64_t v) {
+    return (v >> 11) * (1.0/9007199254740992.0);
+}
+
+HCRYPTPROV bmx_secure_init() {
+    HCRYPTPROV prov;
+    CryptAcquireContext(&prov, NULL, NULL, PROV_RSA_FULL, CRYPT_VERIFYCONTEXT);
+    return prov;
+}
+
+void bmx_secure_destroy(HCRYPTPROV prov) {
+    CryptReleaseContext(prov, 0);
+}
+
+uint64_t bmx_secure_random(HCRYPTPROV prov) {
+    uint64_t result;
+    CryptGenRandom(prov, sizeof(result), (BYTE *)&result);
+    return result;
+}
+
+double bmx_secure_next_double(HCRYPTPROV prov) {
+	return uint64_to_double(bmx_secure_random(prov));
+}